题目内容
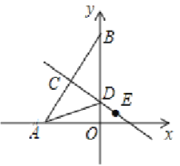
【题目】如图，在平面直角坐标系中，点
，点
，点
在线段
上，点
在
轴上，将
沿直线
翻折，使点
与点
重合．若点
在线段延长线上，且
，点
在轴上，点
在坐标平面内，如果以点
为顶点的四边形是菱形，那么点有（ ）
A.2个B.3个C.4个D.5个
【答案】D
【解析】
根据菱形的性质，分别以EC为边和EC为对角线进行讨论即可得出答案．
∵点
，点
，
∴
，
．
由折叠可知，CE是线段AB的垂直平分线，点C为AB中点，
∴
．
∵以点
为顶点的四边形是菱形，
若CE为菱形的边，则菱形的每个边的长度都为5，分别以点C,E为圆心，以5为半径画圆，所画的圆与y轴有4个交点，分别对应图中的
，即此时对应的N点也有4个，分别为
；
若以CE为菱形的对角线，根据菱形的性质可知，菱形的对角线互相垂直平分，所以先画出CE的垂直平分线，该垂直平分线与y轴的交点即为
，对应的N点即为
．
所以符合条件的N有5个，
故选：D．
练习册系列答案
相关题目
