Question

如图，在湖边有一建筑物和烟囱，某人在建筑物AB的顶A处测得烟囱CD的顶C的仰角为45°，测得C在湖中的倒影E的俯角为60°，已知AB=20米，求烟囱CD的高．（结果保留根号）

Answer 1

分析：作AF⊥CE于F，则直角△ACF和直角△AEF有公共边AF，在两个直角三角形中，利用三角函数即可用AF表示出CF与EF，在直角△AEF中，利用三角函数即可得到一个关于AF的方程，即可求得AF，进而求得CD的长．

解答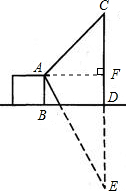：解：作AF⊥CE于F．
则DF=AB=20，设AF=x
Rt△ACF中：∠CAF=45°，
∴CF=AF=x
∴CD=x+20，
∴DE=CD=x+20
∴EF=x+20+20=x+40
Rt△AEF中，∠EAF=60°
由tan60°=

EF

AF

，得：

3

=

x+40

x

解得：x=20

3

+20
∴CD=x+20=20

3

+40米
答：烟囱CD的高是（20

3

+40）米．

点评：本题主要考查了三角形的计算，一般的三角形可以通过作高线转化为解直角三角形的计算，计算时首先计算直角三角形的公共边是常用的思路．