题目内容
如图,一次函数y=ax+b与反比例函数y= 的图象交于A、B两点,与y轴交于C点,与x轴
的图象交于A、B两点,与y轴交于C点,与x轴 交于D点,其中点A(-2,4)、点B(4,-2).
交于D点,其中点A(-2,4)、点B(4,-2).
(1)求这两个函数的表达式;
(2)求证:△AOC≌△BOD.
(1)解:把点A(-2,4)、点B(4,-2)代入一次函数y=ax+b中:
 ,
,
解得: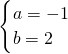 ,
,
∴一次函数解析式为:y=-x+2,
把A(-2,4)代入y= 中,
中,
k=-8,
∴反比例函数解析式为:y=- ;
;
(2)证明:过A作AE⊥x,过B作BF⊥x,
∵A(-2,4)、B(4,-2),
∴OA2=AE2+EO2=42+22=20,
OB2=BF2+FO2=22+42=20,
∴OA=OB,
∴∠OAC=∠OBD,
∵y=-x+2,与x,y交于D,C点,
∴C(0,2),D(2,0),
∴OC=OD,
∴∠OCD=∠ODC,
∴∠ACO=∠BDO,
∴△AOC≌△BOD(AAS).
分析:(1)利用待定系数法把点A(-2,4)、点B(4,-2)代入一次函数y=ax+b,和反比例函数y= 中,即可得到答案;
中,即可得到答案;
(2)首先计算出OA=OB,可得∠OAC=∠OBD,再计算出OC=OD,可得∠OCD=∠ODC,利用等角的补角相等可得∠ACO=∠BDO,便可利用AAS定理证明△AOC≌△BOD.
点评:此题主要考查了待定系数法求一次函数解析式与反比例函数解析式,以及证明三角形全等的判定,证明全等是此题的一个难点,关键是与解析式结合起来求出线段相等,从而得到角相等.
 ,
,解得:
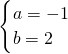 ,
,∴一次函数解析式为:y=-x+2,
把A(-2,4)代入y=
 中,
中,k=-8,
∴反比例函数解析式为:y=-
 ;
;(2)证明:过A作AE⊥x,过B作BF⊥x,

∵A(-2,4)、B(4,-2),
∴OA2=AE2+EO2=42+22=20,
OB2=BF2+FO2=22+42=20,
∴OA=OB,
∴∠OAC=∠OBD,
∵y=-x+2,与x,y交于D,C点,
∴C(0,2),D(2,0),
∴OC=OD,
∴∠OCD=∠ODC,
∴∠ACO=∠BDO,
∴△AOC≌△BOD(AAS).
分析:(1)利用待定系数法把点A(-2,4)、点B(4,-2)代入一次函数y=ax+b,和反比例函数y=
 中,即可得到答案;
中,即可得到答案;(2)首先计算出OA=OB,可得∠OAC=∠OBD,再计算出OC=OD,可得∠OCD=∠ODC,利用等角的补角相等可得∠ACO=∠BDO,便可利用AAS定理证明△AOC≌△BOD.
点评:此题主要考查了待定系数法求一次函数解析式与反比例函数解析式,以及证明三角形全等的判定,证明全等是此题的一个难点,关键是与解析式结合起来求出线段相等,从而得到角相等.

练习册系列答案
相关题目
 已知,如图,一次函数y1=-x-1与反比例函数y2=-
已知,如图,一次函数y1=-x-1与反比例函数y2=-| 2 |
| x |
| A、x>1 |
| B、x<-2或0<x<1 |
| C、-2<x<1 |
| D、-2<x<0或x>1 |
 如图,一次函数y=kx+2的图象与反比例函数y=
如图,一次函数y=kx+2的图象与反比例函数y= 13、如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是
13、如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是 (2013•成都)如图,一次函数y1=x+1的图象与反比例函数
(2013•成都)如图,一次函数y1=x+1的图象与反比例函数 如图,一次函数y=x+3的图象与x轴、y轴分别交于点A、点B,与反比例函数
如图,一次函数y=x+3的图象与x轴、y轴分别交于点A、点B,与反比例函数