题目内容
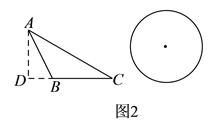
【题目】(![]() )如图
)如图![]() ,
, ![]() 是
是![]() 形内的高,
形内的高, ![]() 是
是![]() 的外接圆⊙
的外接圆⊙![]() 的直径.
的直径.
①求证: ![]() .
.
②若![]() ,
, ![]() ,
, ![]() ,⊙
,⊙ ![]() 的直径
的直径![]() 长.
长.
③如图,在边长为![]() 的小正方形组成的网格之中有一个格点三角形
的小正方形组成的网格之中有一个格点三角形![]() ,请你从上面两小题中获得经验,直接写出此格点三角形的外接圆面积.
,请你从上面两小题中获得经验,直接写出此格点三角形的外接圆面积.
(![]() )如图
)如图![]() ,
, ![]() 是
是![]() 形外的高,若
形外的高,若![]() ,
, ![]() ,
, ![]() ,(
,( ![]() )题中②的结论是否还成立?成立与否都要说明理由.
)题中②的结论是否还成立?成立与否都要说明理由.

【答案】(1)①答案见解析;②![]() ;③
;③![]() ;(2)成立.
;(2)成立.
【解析】试题分析:(1)①由已知条件得到∠ADC=∠ABE=90°,
根据圆周角定理得到∠C=∠E,根据相似三角形的判定定理即可得到△ADC∽△ABE;
②根据相似三角形的性质得到![]() ,即可得到结论;
,即可得到结论;
③根据格点求得S△ABC=7,AC=![]() ,于是得到结论;
,于是得到结论;
(2)设AE是三角形的外接圆的直径,连接BE,根据相似三角形的性质即可得到结论.
试题解析:解:(![]() )①∵
)①∵![]() ,
, ![]() ,∴
,∴ ![]() .
.
②由①可知, ![]() ,则
,则![]() 即
即![]() ,∴
,∴ ![]() .
.
③由图可知:S△ABC=7,AC=![]() ,∴AC边上的高=
,∴AC边上的高=![]() .
.
由①②可知,△ABC的外接圆的半径=![]() ,面积=
,面积=![]() .
.
(![]() )成立,如图所示,过点
)成立,如图所示,过点![]() 作直径
作直径![]() ,⊙
,⊙ ![]() 于点
于点![]() ,
,
连接![]() ,
, ![]() ,则
,则![]() ,∴
,∴ ![]() ,
,
∴![]() ,又
,又![]() ,∴
,∴ ![]() .
.
又∵![]() ,∴
,∴ ![]() ,∴
,∴![]() 即
即![]() ,
, ![]() ,∴结论仍然成立.
,∴结论仍然成立.


练习册系列答案
相关题目