题目内容
【题目】已知二次函数![]() (
(![]() 为非零常数).
为非零常数).
(![]() )若对称轴是直线
)若对称轴是直线![]() .
.
①求二次函数的解析式.
②二次函数![]() (
(![]() 为实数)图象的顶点在
为实数)图象的顶点在![]() 轴上,求
轴上,求![]() 的值.
的值.
(![]() )把抛物线
)把抛物线![]() 向上平移
向上平移![]() 个单位得到新的抛物线
个单位得到新的抛物线![]() ,若
,若![]() ,求
,求![]() 的图像落在
的图像落在![]() 轴上方的部分对应的
轴上方的部分对应的![]() 的取值范围.
的取值范围.
【答案】(1)①![]() ;②
;②![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)①由对称轴是直线x=1,得到![]() ,于是得到结论;②∵二次函数
,于是得到结论;②∵二次函数![]() 图象的顶点在x轴上,列方程得到
图象的顶点在x轴上,列方程得到![]() ;
;
(2)由y=ax 2-ax-x向上平移1个单位得到新的抛物线k 2,得到新的抛物线k 2的解析式为y=ax 2-ax-x+1,解方程得到x 1=1,x 2=![]() ,于是得到结论.
,于是得到结论.
解:(![]() )①∵对称轴为直线
)①∵对称轴为直线![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴二次函数的解析式为![]() .
.
②∵二次函数![]() 图象的顶点在
图象的顶点在![]() 轴上,
轴上,
∴![]() ,
, ![]() .
.
(![]() )∵
)∵![]() 向上平移一个单位长度得到新的抛物线
向上平移一个单位长度得到新的抛物线![]() ,
,
∴![]() 的解析式为
的解析式为![]() ,
,
∴当![]() 时,
时, ![]()
解得![]() ,
, ![]() ,
,
∴![]() 落在
落在![]() 轴上方部分对应的
轴上方部分对应的![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
【题目】为了解某校学生的身高情况,随机抽取该校男生、女生进行调查,已知抽取的样本中,男生和女生的人数相同,利用所得数据绘制如下统计图表:
身高情况分组表(单位:cm)
组别 | 身高 |
|
|
|
|
|
|
|
|
|
|
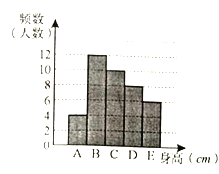
男生身高情况直方图
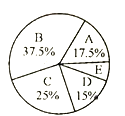
女生身高情况扇形统计图
根据图表提供的信息,回答下列问题:
(1)求样本中男生的人数.
(2)求样本中女生身高在E组的人数.
(3)已知该校共有男生380人,女生320人,请估计全校身高在![]() 之间的学生总人数.
之间的学生总人数.