题目内容
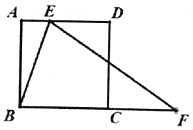
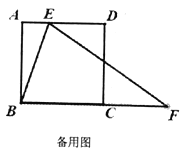
【题目】如图,![]() 是正方形
是正方形![]() 的边
的边![]() 上的动点,
上的动点,![]() 是边
是边![]() 延长线上的一点,且
延长线上的一点,且![]() ,
,![]() ,设
,设![]() ,
,![]() .
.
(1)当![]() 是等边三角形时,求
是等边三角形时,求![]() 的长;
的长;
(2)求![]() 与
与![]() 的函数解析式,并写出它的定义域;
的函数解析式,并写出它的定义域;
(3)把![]() 沿着直线
沿着直线![]() 翻折,点
翻折,点![]() 落在点
落在点![]() 处,试探索:
处,试探索:![]() 能否为等腰三角形?如果能,请求出
能否为等腰三角形?如果能,请求出![]() 的长;如果不能,请说明理由.
的长;如果不能,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)答案见解析.
;(3)答案见解析.
【解析】
(1)当△BEF是等边三角形时,有∠ABE=∠ABC-∠EBC=90°-60°=30°,则可解Rt△ABE,求得BF即BE的长.
(2)作EG⊥BF,垂足为点G,则四边形AEGB是矩形,在Rt△EGF中,由勾股定理知,EF2=(BF-BG)2+EG2.即y2=(y-x)2+122.故可求得y与x的关系.
(3)当把△ABE沿着直线BE翻折,点A落在点A'处,应有∠BA'F=∠BA'E=∠A=90°,若△A'BF成为等腰三角形,必须使A'B=A'F=AB=12,有FA′=EF-A′E=y-x=12,故可由(2)得到的y与x的关系式建立方程组求得AE的值.
解:(1)当![]() 是等边三角形时,
是等边三角形时,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)作![]() ,垂足为点
,垂足为点![]() ,
,
根据题意,得![]() ,
,![]() ,
,![]() .
.
∴![]() .
.
∴所求的函数解析式为![]() ;
;
(3)∵![]() ,
,
∴点![]() 落在
落在![]() 上,
上,
∴![]() ,
,![]() ,
,
∴要使![]() 成为等腰三角形,必须使
成为等腰三角形,必须使![]() .
.
而![]() ,
,![]() ,
,
∴![]() ,由(2)关系式可得:
,由(2)关系式可得:![]() ,
,
整理得![]() ,
,
解得![]() ,
,
经检验:![]() 都原方程的根,
都原方程的根,
但![]() 不符合题意,舍去,
不符合题意,舍去,
所以当![]() 时,
时,![]() 为等要三角形.
为等要三角形.
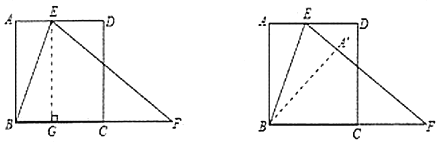

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目