Question

【题目】如图，直线交坐标轴于、两点，交抛物线于点，且是线段的中点，抛物线上另有位于第一象限内的一点，过的直线交坐标轴于、两点，且恰好是线段的中点，若，则点的坐标是________．

Answer 1

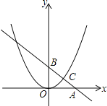
【答案】

【解析】

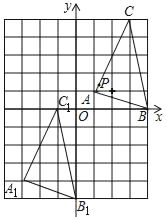
先求出二次函数的解析式,然后根据C为AB中点表示出A,B的坐标,利用三角形相似设出D的坐标并表示出E的坐标,根据P为线段DE的中点表示出P的坐标,代入即可求值.

解：∵抛物线经过点，

∴抛物线的解析式为y=x2,

∵C是线段AB的中点,

∴B(0,6),A(8,0)

∵△AOB∽△DOE

∴

设点D的坐标为（0,a）,则点E的坐标为（,0）,

∵点P为DE的中点,

∴点P的坐标为（,）,

∵点P在抛物线y=x2上,

∴（）2,

解得：a=,

∴P点坐标.