Question

【题目】如图所示，一段街道的两边沿所在直线分别为AB，PQ，并且AB∥PQ，建筑物的一端DE所在的直线MN⊥AB于点M，交PQ于点N，小亮从胜利街的A处，沿着AB方向前进，小明一直站在点P的位置等待小亮．

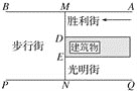
(1)请你画出小亮恰好能看见小明的视线，以及此时小亮所在的位置(用点C标出)．

(2)已知：MN＝30 m，MD＝12 m，PN＝36 m．求(1)中的点C到胜利街口的距离．

Answer 1

【答案】（1）详见解析；（2）点C到胜利街口的距离CM为24 m.

【解析】

（1）根据生活常实作出图形；

（2）由相似三角形性质求出.

解　(1)如图所示，CP为视线，点C为所求位置．

(2)∵AB∥PQ，MN⊥AB于M，

∴∠CMD＝∠PND＝90°.

又∵∠CDM＝∠PDN，

∴△CDM∽△PDN，

∴＝.

∵MN＝30 m，MD＝12 m，

∴ND＝18 m.

∴＝，

∴CM＝24(m)．

∴点C到胜利街口的距离CM为24 m.