题目内容
已知二次函数y=ax2+bx的图象经过点A(-5,0)和点B,其中点B在第一象限,且OA=OB,tan∠BAO=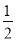
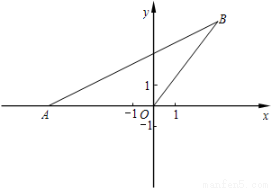
(1)求点B的坐标。
(2)求二次函数的解析式。
(3)过点B作直线BC平行于x轴,直线BC与二次函数图象的另一个交点为C,连结AC,如果点P在x轴上,且△ABC和△PAB相似,求点P的坐标。
(1)点B的坐标是(3,4),(2)y=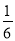 x2+
x2+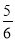 x;(3)点P的坐标为(6,0)或(
x;(3)点P的坐标为(6,0)或(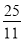 ,0).
,0).
【解析】
试题分析:(1)过点B作BD⊥x轴,垂足为点D,根据余切的定义可设BD=x,AD=2x,在Rt△ODB中根据勾股定理可计算出x,则BD=4,OD=3,所以点B的坐标是(3,4);
(2)利用待定系数法可确定二次函数的解析式;
(3)先确定C点的坐标为(-8,4),则BC=11,AB=4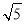 ,由CB∥x轴得到∠ABC=∠BAP,再分类讨论:当△ABC∽△BAP;当△ABC∽△PAB,然后利用比例线段求AP的长,从而确定P点坐标.
,由CB∥x轴得到∠ABC=∠BAP,再分类讨论:当△ABC∽△BAP;当△ABC∽△PAB,然后利用比例线段求AP的长,从而确定P点坐标.
试题解析:(1)过点B作BD⊥x轴,垂足为点D,如图,
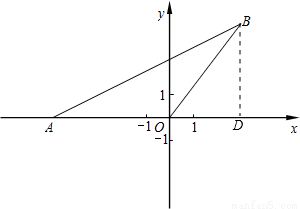
在Rt△ADB中,∠ADB=90°,tan∠BAO=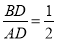
设BD=x,AD=2x,
∵OA=0B=5,
∴OD=2x-5,
在Rt△ODB中,∵OD2+BD2=OB2,
∴(2x-5)2+x2=52,
解得x1=4,x2=0(不合题意,舍去),
∴BD=4,OD=3,
∴点B的坐标是(3,4),
(2)根据题意得
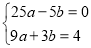 ,
,
解这个方程组,得
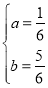 ,
,
∴二次函数的解析式是y=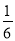 x2+
x2+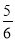 x;
x;
(3)∵直线BC平行于x轴,
∴C点的纵坐标为4,
设C点的坐标为(m,4).
由题意得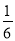 m2+
m2+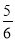 m=4,
m=4,
解得m1=3(不合题意,舍去),m2=-8,
∴C点的坐标为(-8,4),BC=11,AB=4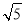
∵∠ABC=∠BAP,
①如果△ABC∽△BAP,那么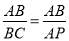
∴AP=11,点P的坐标为(6,0),
②如果△ABC∽△PAB,那么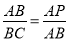 ,
,
∴AP=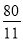 ,点P的坐标为(
,点P的坐标为(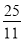 ,0),
,0),
综上所述,点P的坐标为(6,0)或(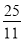 ,0).
,0).
考点:待定系数法求二次函数解析式.

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
 B.
B.
 D.
D.
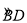 的中点,CE⊥AB于 E,BD交CE于点F.
的中点,CE⊥AB于 E,BD交CE于点F.
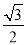 ,cosB=
,cosB=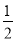 ,则∠C= .
,则∠C= . B.
B. C.
C. D.
D.