题目内容
如图，在菱形ABCD中，AB＝2，∠DAB＝60°，点E是AD边上的
中点，点M是AB边上一动点(不与点A重合)，延长ME交射线CD于点N，连接MD、AN.
(1)求证：四边形AMDN是平行四边形．
(2)填空：①当AM的值为______时，四边形AMDN矩形；
②当AM的值为______时，四边形AMDN是菱形．
(1)证明：∵四边形ABCD是菱形，∴ND∥AM.
∴∠NDE＝∠MAE，∠DNE＝∠AME.又∵点E是AD边的中点，
∴DE＝AE.∴△NDE≌△MAE，∴ND＝MA∴四边形AMDN是平行四边形．(6分)
(2)①1；②2(10分)
练习册系列答案
阅读快车系列答案
相关题目
△ABC中，AB=AC，BD和CE分别是∠ABC和∠ACB的角平分线。则△ABD和哪个三角形全等？为什么？△BEC和哪个三角形全等？为什么？ 随着我国汽车产业的发展，城市道路拥堵问题日益严峻，某部门对15个城市的交通状况进行了调查，得到的数据如下表所示．
| 城市 项目 | 北京 | 太原 | 杭州 | 沈阳 | 广州 | 深圳 | 上海 | 桂林 | 南通 | 海口 | 南京 | 温州 | 威海 | 兰州 | 中山 |
| 上班花费时间（分钟） | 52 | 33 | 34 | 34 | 48 | 46 | 47 | 23 | 24 | 24 | 37 | 25 | 24 | 25 | 18 |
| 上班堵车时间（分钟） | 14 | 12 | 12 | 12 | 12 | 11 | 11 | 7 | 7 | 6 | 6 | 5 | 5 | 5 | 0 |
（1）根据上班花费时间，将下面的频数分布直方图（如图10）补充完整；
图10
（2）求15个城市的平均上班堵车时间（计算结果保留一位小数）；
（3）规定：城市的堵车率=
×100%，比如，北京的堵车率=
×100%≈36.8%；沈阳的堵车率=
×100%≈54.5%，某人欲从北京，沈阳，上海，温州四个城市中任意选取两个作为出发目的地，求选取的两个城市的堵车率都超过30%的概率．
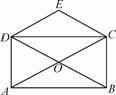
N翻折后，顶点C恰好落在AB边上的点D处，已知MN∥AB，MC＝6，NC＝2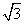
，则四边形MAB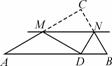
＝
的解为( )
C．－
1 D．无解
图，那么他所画的三视图中的俯视图应该是( )