题目内容
8.画出直线y=$\frac{1}{2}$x+1的图象,利用图象,求:(1)当x<0时,y的取值范围;
(2)当y<0时,x的取值范围;
(3)当-1≤y≤4时,对应的x的取值范围.
分析 分别令x=0、y=0求出一次函数y=$\frac{1}{2}$x+1与两坐标轴的交点,过此两点画出函数图象,根据函数图象即可解答.
解答  解:令x=0,则y=1,令y=0,则x=-2,
解:令x=0,则y=1,令y=0,则x=-2,
故过(0,1)、(-2,0),
两点即可画出一次函数y=-2x+5的图象;
(1)由函数的图象可知,当x<0时,y<1;
(2)由函数的图象可知,当y<0时,x<-2;
(3)由函数的图象可知,当y=-1时,x=-4,
当y=4时,x=6.
故当-1≤y≤4时,-4≤x≤6.
点评 本题考查了一次函数的图象、一次函数图象上点的坐标特征等.一次函数的图象是一直线,根据“两点确定一条直线”来作图.

练习册系列答案
相关题目
16.下列说法正确的是( )
| A. | 掷一枚均匀的骰子,骰子停止运动后,6点朝上是必然事件 | |
| B. | 太阳从西边升起是不可能事件 | |
| C. | “明天降雨的概率为$\frac{1}{2}$”,表示明天有半天都在降雨 | |
| D. | 一个游戏中奖的概率是$\frac{1}{100}$,则做100次这样的游戏一定会中奖 |
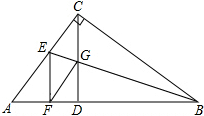 如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,BE平分∠ABC交CD、AC分别于G、E,GF∥AC交AB于F.
如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,BE平分∠ABC交CD、AC分别于G、E,GF∥AC交AB于F.