Question

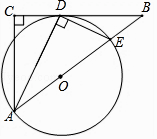
【题目】如图，直线AB，CD相交于点O，OD平分∠BOE，OF平分∠AOE

（1）判断OF与OD的位置关系，并进行证明．

（2）若∠AOC：∠AOD＝1：5，求∠EOF的度数．

Answer 1

【答案】（1）OF⊥OD，证明详见解析；（2）∠EOF＝60°．

【解析】

（1）由OD平分∠BOE、OF平分∠AOE，可得出∠FOE＝∠AOE、∠EOD＝∠EOB，根据邻补角互补可得出∠AOE+∠EOB＝180°，进而可得出∠FOD＝∠FOE+∠EOD＝90°，由此即可证出OF⊥OD；

（2）由∠AOC：∠AOD＝1：5结合邻补角互补、对顶角相等，可求出∠BOD的度数，根据OD平分∠BOE、OF平分∠AOE，可得出∠BOE的度数以及∠EOF＝∠AOE，再根据邻补角互补结合∠EOF＝∠AOE，可求出∠EOF的度数．

（1）OF⊥OD．

证明：∵OD平分∠BOE，OF平分∠AOE，

∴∠FOE＝∠AOE，∠EOD＝∠EOB．

∵∠AOE+∠EOB＝180°，

∴∠FOD＝∠FOE+∠EOD＝（∠AOE+∠EOB）＝90°．

∴OF⊥OD．

（2）∵∠AOC：∠AOD＝1：5，∠AOC＝∠BOD，

∴∠BOD：∠AOD＝1：5．

∵∠AOD+∠BOD＝180°，

∴∠BOD＝30°，∠AOD＝150°．

∵OD平分∠BOE，OF平分∠AOE，

∴∠BOE＝2∠BOD＝60°，∠EOF＝∠AOE．

∵∠AOE+∠BOE＝180°，

∴∠AOE＝120°，

∴∠EOF＝60°．