题目内容
AB是圆O的直径，C是圆上一点，CD⊥AB于点D，CE、BE是圆O的切线，点C、B是切点，连接AE，交CD于点P，求证：PC=PD．
考点：切线的性质
专题：证明题
分析：过点A作⊙O的切线交EC的延长线于H，如图，根据切线的性质得AH⊥AB，EB⊥AB，易得AH∥CD∥BE，利用平行线分线段成比例定理得到
=
，再证明△ECP∽△EHA得到PC=
，证明△ADP∽△ABE，得到
=
，代换后得
=
，则PD=
，然后根据切线长定理得到HA=HC，EC=EB，所以PC=PD．
| AD |
| AB |
| HC |
| HE |
| EC•AH |
| EH |
| PD |
| BE |
| AD |
| AB |
| PD |
| BE |
| HC |
| HE |
| BE•HC |
| EH |
解答：证明：过点A作⊙O的切线交EC的延长线于H，如图，
∵AH、BE为⊙O的切线，
∴AH⊥AB，EB⊥AB，
而CD⊥AB，
∴AH∥CD∥BE，
∴
=
，
∵PC∥AH，
∴△ECP∽△EHA，
∴
=
，即PC=
，
∵PD∥BE，
∴△ADP∽△ABE，
∴
=
，
∴
=
，即PD=
，
∵EH、EB、HA为⊙O的切线，
∴HA=HC，EC=EB，
∴PC=PD．
∵AH、BE为⊙O的切线，
∴AH⊥AB，EB⊥AB，
而CD⊥AB，
∴AH∥CD∥BE，
∴
| AD |
| AB |
| HC |
| HE |
∵PC∥AH，
∴△ECP∽△EHA，
∴
| PC |
| AH |
| EC |
| EH |
| EC•AH |
| EH |
∵PD∥BE，
∴△ADP∽△ABE，
∴
| PD |
| BE |
| AD |
| AB |
∴
| PD |
| BE |
| HC |
| HE |
| BE•HC |
| EH |
∵EH、EB、HA为⊙O的切线，
∴HA=HC，EC=EB，
∴PC=PD．
点评：本题考查了切线的性质：圆的切线垂直于经过切点的半径．也考查了切线长定理、相似三角形的判定与性质和平行线分线段成比例定理．运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题．
练习册系列答案
相关题目
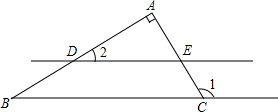如图，∠1是△ABC的一个外角，∠A=90°，直线DE∥BC，分别交AB，AC于点D，E，∠1=120°，求∠2的度数．
小强、小红俩兄妹是香市中学的学生，某天，兄妹俩决定比比看谁先到家，小强让小红先走，图中两条线段分别表示小强，小红回家过程中离学校的距离S（米）以及回家所用的时间T（分）的关系，请根据图象回答：
如图，已知等腰直角△ABC和等腰直角△ADE有公共直角顶点，P是△ADE内一点，PB=PD，PC=PE，求∠BPC+∠DPE的度数．