Question

已知AD是Rt△ABC的角平分线，∠CAB=90°，BC=18，tanB=，那么BD=________．

Answer 1

12
分析：延长BA到E，使AE=AC，连接CE，得到等腰直角三角形ACE，则∠E=∠BAD=45°，CE∥AD，再根据和平行线分线段成比例定理得出CD：BD=AC：AB，结合三角函数的定义得出CD：DB=1：2，然后由
BC=18即可求解．
解答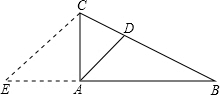：解：如图，延长BA到E，使AE=AC，连接CE，则∠E=∠ECA=45°．
∵∠CAD=∠BAD=45°，
∴∠E=∠BAD=45°，
∴CE∥AD，
∴CD：BD=AE：AB，
∵AC=AE，
∴CD：BD=AC：AB，
∵AC：AB=tanB=，
∴CD：DB=1：2，即DB=2CD，
∵DB+CD=BC=18，
∴CD=6，BD=12．
故答案为：12．
点评：本题考查了解直角三角形，三角函数，通过作辅助线，得到CE∥AD，构造比例线段进行转换，考查了灵活运用知识的能力．