题目内容

代数式a2-2a-2的最小值为（　　）
A、-4B、-3C、3D、2
考点：配方法的应用,非负数的性质：偶次方
专题：
分析：原式配方变形后，利用非负数的性质即可求出最小值．
解答：解：∵a2-2a-2=（a-1）2-3≥-3．
∴代数式a2-2a-2的最小值为-3．
故选：B．
点评：此题考查了配方法的应用，以及非负数的性质，熟练掌握完全平方公式是解本题的关键．
练习册系列答案
相关题目
已知x2-7x-15=（x+m）（x+n），则m+n=
 
．
若3x2a+b+1-5ya-2b-1=10是关于x，y的二元一次方程，则a=
 
，b=
 
．
把方程2x-y=5变形，用含x的代数式表示y=
 
；用含y的代数式表示x=
 
．
长方形周长为30，设长为x，宽为y，则y与x的函数关系式为（　　）
A、y=30-x
B、y=30-2x
C、y=15-x
D、y=15+2x
已知
x=1
y=-1
是方程2x-3=ay的一个解，则a的值为（　　）
A、1B、3C、一2D、一1
如图，矩形ABCD的两条对角线相交于点O，∠AOD=120°，AB=2，则矩形的对角线AC的长是（　　）
A、2
B、4
C、2
3
D、4
3
若y=（m-1）xm2+1+3x+1是二次函数，则m的值是（　　）
A、1B、-1C、±1D、0
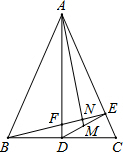如图，在△ABC中，AB=AC，AD⊥BC于点D，DE⊥AC于点E，M为DE中点，AM与BE相交于点N，AD与BE相交于点F．求证：
（1）
DE
CE
=
AD
CD
；
（2）△BCM∽△ADM；
（3）AM⊥BE．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网