题目内容
某工程指挥部街道甲、乙两个工程队关于完成某个工程的投标书，从投标书中得知：甲工程队单独完成这项工程所需天数是乙工程队单独完成这项所需天数的
；若先由甲工程队做15天，则剩下的工程再由甲、乙两个工程队合做15天可以完成．
（1）求甲、乙两个工程队单独完成这项工程分别需要多少天？
（2）已知甲工程队每天的施工费用为0.84万元，乙工程队每天的施工费用为0.56万元．工程预算的施工费用为33万元，为缩短工期以减少对住户的影响，拟安排甲、乙两个工程队合作完成这项工程，则工程预算的施工费用是否够用？若不够用，需追加预算多少万元？请给出你的判断，并说明理由．
解：设乙队单独完成这项工程需要x天，则甲队单独完成这项工程需要x天，根据题意得：
•（15+15）+
•15=1
解得：x=60，
经检验x=60分式方程的解，
则甲队单独完成这项工程需要的天数是：60×=40（天）．
答：甲需要40天，乙需要60天．
（2）设甲、乙两队合作，完成这项工程需y天，则：
y（
+
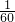）=1，
解得y=24，
需要施工费用 （0.84+0.56）×24=33.6（万元）．
∵33.6＞33，
∴工程预算的费用不够用，需追加0.6万元．
分析：（1）设乙队单独完成这项工程需要x天，则甲队单独完成这项工程需要x天，根据由甲队先做10天，剩下的工程再由甲、乙两队合作30天可以完成客人列方程求解．
（2）求出甲、乙两队施工天数得出需要施工费用，再与33万元进行比较，即可得出答案．
点评：此题主要考查了分式方程的应用，列方程解应用题的关键步骤在于找相等关系，找到关键描述语，找到等量关系，列出方程．
x天，根据题意得：•（15+15）+•15=1解得：x=60，
经检验x=60分式方程的解，
则甲队单独完成这项工程需要的天数是：60×
=40（天）．答：甲需要40天，乙需要60天．
（2）设甲、乙两队合作，完成这项工程需y天，则：
y（
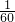+）=1，解得y=24，
需要施工费用 （0.84+0.56）×24=33.6（万元）．
∵33.6＞33，
∴工程预算的费用不够用，需追加0.6万元．
分析：（1）设乙队单独完成这项工程需要x天，则甲队单独完成这项工程需要
x天，根据由甲队先做10天，剩下的工程再由甲、乙两队合作30天可以完成客人列方程求解．（2）求出甲、乙两队施工天数得出需要施工费用，再与33万元进行比较，即可得出答案．
点评：此题主要考查了分式方程的应用，列方程解应用题的关键步骤在于找相等关系，找到关键描述语，找到等量关系，列出方程．
练习册系列答案
相关题目
注意：为了使同学们更好地解答本题，我们提供了一种解题思路，你可以依照这个思路，填写表格，并完成本题解答过程．如果你选用其它的解题方案，此时，不必填写表格，只需按照解答题的一般要求，进行解答即可．
我市街道改建工程指挥部，要对某路段工程进行招标，接到了甲、乙两个工程队的投标书，从投标书中可得知：甲队单独做比甲、乙两队合作完成的天数多5天．如果甲、乙两队先合作4天，再由乙队独做3天后，才完成工程的一半，问甲、乙两队合作，甲队独做各需要多少天完工？
（Ⅰ）设甲、乙两队合作要x天完工，根据题意，利用工作效率、工作时间、工作量间的关系填写下表．（要求：填上适当的代数式，完成表格）
（Ⅱ）列方程（组），并求出问题的解．
我市街道改建工程指挥部，要对某路段工程进行招标，接到了甲、乙两个工程队的投标书，从投标书中可得知：甲队单独做比甲、乙两队合作完成的天数多5天．如果甲、乙两队先合作4天，再由乙队独做3天后，才完成工程的一半，问甲、乙两队合作，甲队独做各需要多少天完工？
（Ⅰ）设甲、乙两队合作要x天完工，根据题意，利用工作效率、工作时间、工作量间的关系填写下表．（要求：填上适当的代数式，完成表格）
| 工作效率 | 工作时间 | 工作量 | |
| 甲 | 4 | ||
| 乙 | 4+3 | ||
| 两队合作 | x | 1 |