题目内容
已知y=|x-1|+2|x-3|+4|x-4|，求y的最小值．
考点：绝对值函数的最值
专题：
分析：利用x的取值不同分别得出函数的最小值，进而得出答案．
解答：解：当x＜1时，则y=1-x+2（3-x）+4（4-x）=19-6x，则最小值为13；
当1≤x＜3时，则y=x-1+2（3-x）+4（4-x）=21-5x，则最小值为6；
当3≤x＜4时，则y=x-1+2（x-3）+4（4-x）=9-x，则最小值为5；
当x≥4时，则y=x-1+2（x-3）+4（x-4）=7x-23，则最小值为5；
故y的最小值为5．
当1≤x＜3时，则y=x-1+2（3-x）+4（4-x）=21-5x，则最小值为6；
当3≤x＜4时，则y=x-1+2（x-3）+4（4-x）=9-x，则最小值为5；
当x≥4时，则y=x-1+2（x-3）+4（x-4）=7x-23，则最小值为5；
故y的最小值为5．
点评：此题主要考查了绝对值函数最值求法，利用分类讨论得出是解题关键．
练习册系列答案
相关题目
下列各式中能用平方差公式是（ ）
| A、（x+y）（y+x） |
| B、（x+y）（y-x） |
| C、（x+y）（-y-x） |
| D、（-x+y）（y-x） |
多项式b2n-bn提公因式bn后，另一个因式是（ ）
| A、bn-1 |
| B、b2n-1-1 |
| C、b2n-1 |
| D、bn |
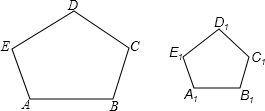如图所示，在五边形ABCDE与五边形A1B1C1D1E1中，∠A=∠A1，∠B=∠B1，且
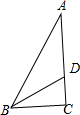如图，Rt△ABC中，∠C=90°，AC=6，∠A=30°，BD平分∠ABC交AC于点D，求点D到斜边AB的距离．
如图，△ABC中，CD⊥AB于D，点F在BC上，连接AF交CD于点E，已知AD=CD，DE=DB，AE=4．