题目内容
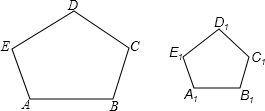如图所示，在五边形ABCDE与五边形A1B1C1D1E1中，∠A=∠A1，∠B=∠B1，且| AB |
| A1B1 |
| BC |
| B1C1 |
| CD |
| C1D1 |
| DE |
| D1E1 |
| EA |
| E1A1 |
考点：相似多边形的性质
专题：证明题
分析：连接BE、CE，B1E1、C1E1，根据两边对应成比例，夹角相等，两三角形相似求出△ABE和△A1B1E1相似，根据相似三角形对应边成比例可得
=
=
，相似三角形对应角相等可得∠ABE=∠A1B1E1，再求出∠EBC=∠E1B1C1，然后求出△EBC和△E1B1C1相似，根据相似三角形对应边成比例可得
=
，再求出△CDE和△C1D1E1相似，从而得证．
| BE |
| B1E1 |
| AB |
| A1B1 |
| BC |
| B1C1 |
| EC |
| E1C1 |
| BC |
| B1C1 |
解答：
证明：如图，连接BE、CE，B1E1、C1E1，
∵
=
，∠A=∠A1，
∴△ABE∽△A1B1E1，
∴
=
=
，∠ABE=∠A1B1E1，
∵∠B=∠B1，
∴∠EBC=∠E1B1C1，
∴△EBC∽△E1B1C1，
∴
=
，
∴
=
=
，
∴△CDE∽△C1D1E1，
综上所述，两个五边形被分成的三个三角形对应相似，
∴五边形ABCDE∽五边形A1B1C1D1E1．
证明：如图，连接BE、CE，B1E1、C1E1，∵
| AB |
| A1B1 |
| EA |
| E1A1 |
∴△ABE∽△A1B1E1，
∴
| BE |
| B1E1 |
| AB |
| A1B1 |
| BC |
| B1C1 |
∵∠B=∠B1，
∴∠EBC=∠E1B1C1，
∴△EBC∽△E1B1C1，
∴
| EC |
| E1C1 |
| BC |
| B1C1 |
∴
| EC |
| E1C1 |
| CD |
| C1D1 |
| DE |
| D1E1 |
∴△CDE∽△C1D1E1，
综上所述，两个五边形被分成的三个三角形对应相似，
∴五边形ABCDE∽五边形A1B1C1D1E1．
点评：本题考查了多边形的性质，主要利用了相似三角形相似的判定与性质，作辅助线构造出相似三角形是解题的关键．
练习册系列答案
相关题目
（1）如图：是有一些相同小正方体搭建而成的几何体的俯视图，其中小正方形中的数字表示在这个位置小立方体的个数，请画出该几何体的主视图与左视图．
如图，直线l1的解析表达式为y=-3x+3，且l1与x轴交于点A，B；直线l2经过点