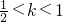题目内容
已知不等边三角形中,有一条边长等于另两边长的平均值,则最大边上的高与最小边上的高的比值k的取值范围是( )
A.
| B.
| C.1<k<2 | D.
|
设a>b>c
k=
:
=c:a
∴c:a<1
又因为a+c=2b①
又∵a-c<b②
2a<3b,a<
b
c>
b
c:a>
所以,
<k<1.
故选D.
k=
| 1 |
| a |
| 1 |
| c |
∴c:a<1
又因为a+c=2b①
又∵a-c<b②
2a<3b,a<
| 3 |
| 2 |
c>
| 1 |
| 2 |
c:a>
| 1 |
| 3 |
所以,
| 1 |
| 3 |
故选D.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
已知不等边三角形中,有一条边长等于另两边长的平均值,则最大边上的高与最小边上的高的比值k的取值范围是( )
A、
| ||
B、
| ||
| C、1<k<2 | ||
D、
|