题目内容
已知不等边三角形中,有一条边长等于另两边长的平均值,则最大边上的高与最小边上的高的比值k的取值范围是
- A.

- B.
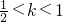
- C.1<k<2
- D.

D
分析:可设三角形三边a>b>c,根据三角形的面积公式可知最大边上的高与最小边上的高的比为c:a<1,再根据已知和三角形三边关系可知c:a> ,则最大边上的高与最小边上的高的比值k的取值范围可求.
,则最大边上的高与最小边上的高的比值k的取值范围可求.
解答:设a>b>c
k= :
: =c:a
=c:a
∴c:a<1
又因为a+c=2b①
又∵a-c<b②
2a<3b,a< b
b
c> b
b
c:a>
所以, <k<1.
<k<1.
故选D.
点评:本题综合考查了三角形的面积公式和三角形三边关系及解不等式,有一定的难度,解题的关键是得出三角形最大边上的高与最小边上的高的比等于最小边与最大边的比.
分析:可设三角形三边a>b>c,根据三角形的面积公式可知最大边上的高与最小边上的高的比为c:a<1,再根据已知和三角形三边关系可知c:a>
 ,则最大边上的高与最小边上的高的比值k的取值范围可求.
,则最大边上的高与最小边上的高的比值k的取值范围可求.解答:设a>b>c
k=
 :
: =c:a
=c:a∴c:a<1
又因为a+c=2b①
又∵a-c<b②
2a<3b,a<
 b
bc>
 b
bc:a>

所以,
 <k<1.
<k<1.故选D.
点评:本题综合考查了三角形的面积公式和三角形三边关系及解不等式,有一定的难度,解题的关键是得出三角形最大边上的高与最小边上的高的比等于最小边与最大边的比.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
已知不等边三角形中,有一条边长等于另两边长的平均值,则最大边上的高与最小边上的高的比值k的取值范围是( )
A、
| ||
B、
| ||
| C、1<k<2 | ||
D、
|

