题目内容
 如图,已知反比例函数y=
如图,已知反比例函数y=| m |
| x |
(1)求a的值与反比例函数的解析式;
(2)观察图象,写出在第一象限内,x取何值时x+a的值大于
| m |
| x |
(3)将直线y=x+a向上平移后与反比例函数的图象相交于点C,且△ABC的面积为8,求平移后的直线的函数关系式.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)把点B(-2a,a+2)代入一次函数y=x+a中,即可求得a的值,从而得出B(2,1),代入反比例函数y=
(x>0)中,即可求得m的值,从而求得解析式;
(2)通过观察图象即可求得x+a的值大于
的值的x的取值;
(3)设平移后直线解析式为y=x+b,C(n,n+b),根据直线y=x-1,求得OA=1,过C作CD⊥y轴,过B作BE⊥y轴,将C坐标代入反比例解析式得n(n+b)=2,根据S△ABC=S梯形BCDE+S△ABE-S△ACD=8,即可求得b的值,从而求得平移后的直线的函数关系式.
| m |
| x |
(2)通过观察图象即可求得x+a的值大于
| m |
| x |
(3)设平移后直线解析式为y=x+b,C(n,n+b),根据直线y=x-1,求得OA=1,过C作CD⊥y轴,过B作BE⊥y轴,将C坐标代入反比例解析式得n(n+b)=2,根据S△ABC=S梯形BCDE+S△ABE-S△ACD=8,即可求得b的值,从而求得平移后的直线的函数关系式.
解答:解:(1)∵一次函数y=x+a的图象经过点B(-2a,a+2),
∴a+2=-2a+a,
解得a=-1,
∴B(2,1),
代入y=
(x>0)得1=
,
解得m=2.
∴反比例函数的解析式为y=
;
(2)由于B(2,1),通过观察图象可知当x>2时,x+a的值大于
的值;
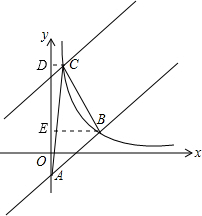
(3)如图,设平移后直线解析式为y=x+b,C(n,n+b),对于直线y=x-1,令x=0求出y=-1,得到OA=1,
过C作CD⊥y轴,过B作BE⊥y轴,将C坐标代入反比例解析式得:n(n+b)=2,
∵S△ABC=S梯形BCDE+S△ABE-S△ACD=8,
∴
×(n+2)×(n+b-1)+
×(1+1)×2-
×n×(n+b+1)=8,
解得b=7,
∴平移后直线的函数解析式为y=x+7,
∴a+2=-2a+a,
解得a=-1,
∴B(2,1),
代入y=
| m |
| x |
| m |
| 2 |
解得m=2.
∴反比例函数的解析式为y=
| 2 |
| x |

(2)由于B(2,1),通过观察图象可知当x>2时,x+a的值大于
| m |
| x |
(3)如图,设平移后直线解析式为y=x+b,C(n,n+b),对于直线y=x-1,令x=0求出y=-1,得到OA=1,
过C作CD⊥y轴,过B作BE⊥y轴,将C坐标代入反比例解析式得:n(n+b)=2,
∵S△ABC=S梯形BCDE+S△ABE-S△ACD=8,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得b=7,
∴平移后直线的函数解析式为y=x+7,
点评:此题考查了一次函数与反比例函数的交点问题,涉及的知识有:一次函数与坐标轴的交点,待定系数法求函数解析式,三角形、梯形的面积求法,以及坐标与图形性质,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
地球的半径是6370km,用科学记数法表示是( )米.
| A、6.37×103 |
| B、637×101 |
| C、63.7×105 |
| D、6.37×106 |