Question

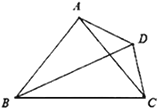
【题目】如图，在四边形ABCD中，AB=AC，BC=BD，若，则______.（用含的代数式）.

Answer 1

【答案】

【解析】

延长DA到E点，使AE=AC，连接BE，易证∠EAB=∠BAC，可得△AEB≌△ABC，则∠E=∠ACB= ，BE=BC=BD，则∠BDE=∠E= ，可证∠DBC=∠DAC=4-180°，即可求得∠BCD的度数.

延长DA到E点，使AE=AC，连接BE

∵AB=AC，

∴∠ACB =∠ABC = ，∠BAD=2

∴∠BAC =180°-2，∠EAB=180°-2

又AB=AB

∴△AEB≌△ABC（SAS）

∴∠E=∠ACB=，BE=BC=BD

∴∠BDE=∠E=

∴∠DBC=∠DAC=∠BAD-∠BAC=2-（180°-2）= 4-180°

∴∠BCD=

故答案为：