题目内容
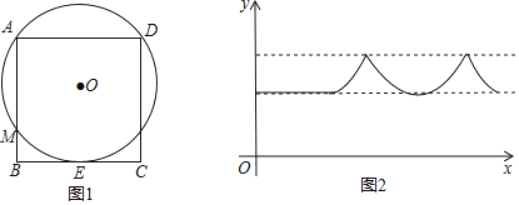
【题目】如图,![]() 、
、![]() 是⊙
是⊙![]() 的切线,
的切线,![]() ,
,![]() 为切点,
为切点,![]() .连接
.连接![]() 并延长与⊙
并延长与⊙![]() 交于
交于![]() 点,连接
点,连接![]() 、
、![]() .
.
(1)求证:四边形![]() 是菱形.
是菱形.
(2)若⊙![]() 半径为1,求菱形
半径为1,求菱形![]() 的面积.
的面积.

【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连接AO,BO,根据PA、PB是⊙O的切线,得到∠OAP=∠OBP=90°,PA=PB,∠APO=∠BPO=![]() ∠APB=30°,由三角形的内角和得到∠AOP=60°,根据三角形外角的性质得到∠ACO=30°,得到AC=AP,同理BC=PB,于是得到结论;
∠APB=30°,由三角形的内角和得到∠AOP=60°,根据三角形外角的性质得到∠ACO=30°,得到AC=AP,同理BC=PB,于是得到结论;
(2)连接AB交PC于D,根据菱形的性质得到AD⊥PC,解直角三角形即可得到结论.
(1)连接AO,BO,

∵PA、PB是⊙O的切线,
∴∠OAP=∠OBP=90°,PA=PB,∠APO=∠BPO=![]() ∠APB=30°,
∠APB=30°,
∴∠AOP=60°,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠AOP=∠CAO+∠ACO,
∴∠ACO=30°,
∴∠ACO=∠APO,
∴AC=AP,
同理BC=PB,
∴AC=BC=BP=AP,
∴四边形ACBP是菱形;
(2)连接AB交PC于D,
∴AD⊥PC,
∴OA=1,∠AOP=60°,
∴AD=![]() OA=
OA=![]() ,
,
∴PD=![]() ,
,
∴PC=3,AB=![]() ,
,
∴菱形ACBP的面积=![]() ABPC=
ABPC=![]() .
.

练习册系列答案
相关题目