ЬтФПФкШн
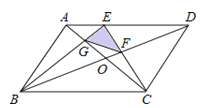
ЁОЬтФПЁПШчЭМЃЌдкСтаЮABCDжаЃЌЁЯB= 60Ёу.
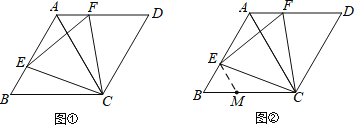
ЃЈ1ЃЉШчЭМЂй.ШєЕуEЁЂFЗжБ№дкБпABЁЂADЩЯЃЌЧвBE=AFЃЌЧѓжЄ:ЁїCEFЪЧЕШБпШ§НЧаЮ.
ЃЈ2ЃЉаЁУїЗЂЯжЃЌЕБЕуEЁЂFЗжБ№дкБпABЁЂADЩЯЃЌЧвЁЯCEF=60ЁуЪБЃЌЁїCEFвВЪЧЕШБпШ§НЧаЮЃЌ
ВЂЭЈЙ§ЛЭМбщжЄСЫВТЯы;аЁРіЭЈЙ§ЬНЫїЃЌШЯЮЊгІИУвдCE= EFЮЊЭЛЦЦПкЃЌЙЙдьСНИіШЋЕШШ§НЧаЮ:аЁйЛЪмЕНаЁРіЕФЦєЗЂЃЌГЂЪддкBCЩЯНиШЁBM =BEЃЌВЂСЌНгMEЃЌШчЭМЂкЃЌКмПьОЭжЄУїСЫЁїCEFЪЧЕШБпШ§НЧаЮ.ЧыФуИљОнаЁйЛЕФЗНЗЈЃЌаДГіЭъећЕФжЄУїЙ§ГЬ.
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉМћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉвзжЄЁїBECЁеЁїAFCЃЌМДПЩЕУжЄЃЛЃЈ2ЃЉЯШжЄЕУЁїBEMЪЧЕШБпШ§НЧаЮЃЌдйжЄЁїMECЁеAFEЃЌМДПЩEC=EFЃЌдйгЩЁЯCEF=60ЁуМДПЩжЄУї.
ЃЈ1ЃЉвђЮЊЫФБпаЮABCDЪЧСтаЮЃЌЫљвдAB= BC=CD=AD.
вђЮЊЁЯB=60ЁуЃЌЫљвдЁїABCЃЌЁїADCЖМЪЧЕШБпШ§НЧаЮ.
ЫљвдBC=ACЃЌЁЯB=ЁЯCAF=ЁЯACB=60ЁуЃЌ
гжвђЮЊBE=AFЃЌЫљвд.ЁїBECЁеЁїAFC(SAS)ЃЌЫљвдCE=CFЃЌЁЯECF=ЁЯBCA=60Ёу
ЫљвдЁїECFЪЧЕШБпШ§НЧаЮЃЌ
(2) вђЮЊBE=BMЃЌЁЯB= 60Ёу
ЫљвдЁїBEMЪЧЕШБпШ§НЧаЮ.
ЫљвдЁЯEMB=ЁЯBEM=60ЁуЃЌЁЯEMC=ЁЯAEM=120Ёу
вђЮЊAB= BCЃЌЁЯEAF120ЁуЃЌЫљвд.AE=CMЃЌЁЯEAF=ЁЯEM.
вђЮЊЁЯFEC=60ЁуЃЌЫљвдЁЯAEF+ЁЯCEM=60Ёу.
гжвђЮЊЁЯCEM+ЁЯECM=60ЁуЫљвдЁЯAEF=ЁЯECM.
ЫљвдЁїMECЁеAFE(ASA)ЃЌЫљвдEC=EF.
гжвђЮЊЁЯFEC=60ЁуЃЌЫљвдЁїEFCЪЧЕШБпШ§НЧаЮ.

ЁОЬтФПЁПФГбЇаЃзМБИЙКТђAЁЂBСНжжаЭКХРКЧђЃЌбЏЮЪСЫМзЁЂввСНМфбЇаЃСЫНтетСНПюРКЧђЕФМлИёЃЌЯТБэЪЧМзЁЂввСНМфбЇаЃЙКТђAЁЂBСНжжаЭКХРКЧђЕФЧщПіЃК
ЙКТђбЇаЃ | ЙКТђаЭКХМАЪ§СПЃЈИіЃЉ | ЙКТђжЇГіПюЯюЃЈдЊЃЉ | |
A | B | ||
Мз | 3 | 8 | 622 |
вв | 5 | 4 | 402 |
ЃЈ1ЃЉЧѓAЁЂBСНжжаЭКХЕФРКЧђЕФЯњЪлЕЅМлЃЛ
ЃЈ2ЃЉШєИУбЇаЃзМБИгУВЛЖргк1000дЊЕФН№ЖюЙКТђетСНжжаЭКХЕФРКЧђЙВ20ИіЃЌЧѓAжжаЭКХЕФРКЧђзюЩйФмВЩЙКЖрЩйИіЃП