题目内容
如图所示,△ABD,△ACE都是等边三角形,求证:CD=BE.
【答案】分析:要证线段相等,可以把这两条线段放到△ADC和△ABE中,考虑证明全等的条件.根据SAS判定全等后答案可得.
解答:证明:∵△ABD,△ACE都是等边三角形,
∴AC=AE,AD=AB.
∵∠EAC=∠DAB=60°,
∠EAC+∠BAC=∠DAB+∠BAC,
即∠EAB=∠CAD.
在△EAB和△CAD中,
AE=AC,∠EAB=∠CAD,AB=AD,
∴△EAB≌△CAD.
∴BE=CD.
点评:本题考查了全等三角形的判定与性质及等边三角形的性质;可围绕结论寻找全等三角形,运用全等三角形的性质判定线段相等,证得∠EAB=∠CAD是正确解答本题的关键.
解答:证明:∵△ABD,△ACE都是等边三角形,
∴AC=AE,AD=AB.
∵∠EAC=∠DAB=60°,
∠EAC+∠BAC=∠DAB+∠BAC,
即∠EAB=∠CAD.
在△EAB和△CAD中,
AE=AC,∠EAB=∠CAD,AB=AD,
∴△EAB≌△CAD.
∴BE=CD.
点评:本题考查了全等三角形的判定与性质及等边三角形的性质;可围绕结论寻找全等三角形,运用全等三角形的性质判定线段相等,证得∠EAB=∠CAD是正确解答本题的关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
 已知:如图所示,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.
已知:如图所示,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°. 19、如图所示,△ABD和△CBD都是等边三角形,AC与BD交于点O,图中全等三角形的对数有( )
19、如图所示,△ABD和△CBD都是等边三角形,AC与BD交于点O,图中全等三角形的对数有( ) 23、如图所示,△ABD,△ACE都是等边三角形,求证:CD=BE.
23、如图所示,△ABD,△ACE都是等边三角形,求证:CD=BE.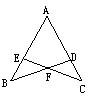 11、(1)已知:如图所示,BD与EC交于F点,AD=AE,∠B=∠C.
11、(1)已知:如图所示,BD与EC交于F点,AD=AE,∠B=∠C. 13、如图所示,△ABD是ABC△沿AB边所在的直线翻折得到的,已知∠C=100°,∠ABC=30°,则∠CAD=
13、如图所示,△ABD是ABC△沿AB边所在的直线翻折得到的,已知∠C=100°,∠ABC=30°,则∠CAD=