题目内容
在△ABC中，已知∠A=30°，∠B是∠A的两倍，∠C等于（ ）
| A、45° | B、60° |
| C、90° | D、120° |
考点：三角形内角和定理
专题：计算题
分析：先计算出∠B=60°，然后根据三角形内角和定理计算∠C的度数．
解答：解：∵∠A=30°，∠B是∠A的两倍，
∴∠B=2×30°=60°，
∵∠A+∠B+∠C=180°，
∴∠C=180°-60°-30°=90°．
故选C．
∴∠B=2×30°=60°，
∵∠A+∠B+∠C=180°，
∴∠C=180°-60°-30°=90°．
故选C．
点评：本题考查了三角形内角和定理：三角形内角和定理：三角形内角和是180°．
练习册系列答案
阅读快车系列答案
相关题目
△ABC中∠A：∠B：∠C=3：5：10，又△A′B′C≌△ABC，且B′、C、A在同一直线上，则∠BC A′：∠BC B′=
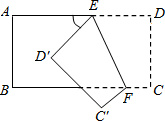如图所示，把一个长方形纸片沿EF折叠后，点D、C分别落在D′、C′的位置．若∠AED′=50°，则∠DEF等于（ ）| A、50° | B、65° |
| C、75° | D、60° |
如果x+
，那么x的取值范围是（ ）
| x+1 |
| A、x=0 | B、x=1 |
| C、x≥-1 | D、x=0或x=1 |
使式子
有意义的实数x的取值范围是（ ）
| 2x+3 |
A、x＞
| ||
B、x＞
| ||
C、x≥-
| ||
D、x≥-
|
在
=
+
中，用u、v表示f，正确的是（ ）
| 1 |
| f |
| 1 |
| u |
| 1 |
| v |
A、
| ||
B、
| ||
| C、u+v | ||
| D、uv |
分解因式8x2-2y2正确是（ ）
| A、2（2x+y）（2x-y） |
| B、（2x+y）（2x-y） |
| C、4（2x+y）（2x-y） |
| D、4（2x+y）2 |
式子
=
成立的条件是（ ）
|
| ||
|
| A、x＜1且x≠0 |
| B、x＞0且x≠1 |
| C、0＜x≤1 |
| D、0＜x＜1 |