题目内容
已知抛物线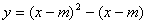 ,其中
,其中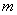 是常数
是常数
(1)求证:不论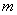 为何值,该抛物线与
为何值,该抛物线与 轴一定有两个公共点;
轴一定有两个公共点;
(2)若该抛物线的对称轴为直线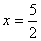 ,
,
①求该抛物线的函数解析式;
②把该抛物线沿 轴向上平移多少个单位长度后,得到的抛物线与
轴向上平移多少个单位长度后,得到的抛物线与 轴只有一个公共点?
轴只有一个公共点?
解:(1)证明:∵ ,
,
∴由 得
得 .
.
∵ ,∴不论
,∴不论 为何值,该抛物线与
为何值,该抛物线与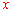 轴一定有两个公共点.
轴一定有两个公共点.
(2)①∵ ,
,
∴抛物线的对称轴为直线 ,解得
,解得 .
.
∴抛物线的函数解析式为 .
.
②∵ .
.
∴该抛物线沿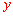 轴向上平移
轴向上平移 个单位长度后,得到的抛物线与
个单位长度后,得到的抛物线与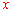 轴只有一个公共点.
轴只有一个公共点.
【考点】抛物线与 轴交点问题;二次函数的性质;二次函数的平移性质.
轴交点问题;二次函数的性质;二次函数的平移性质.
【分析】(1)证明 总有两个不等的实数根即可.
总有两个不等的实数根即可.
(2)①根据对称轴为直线 列方程求解即可.
列方程求解即可.
②把 化为顶点式即可求解.
化为顶点式即可求解.

练习册系列答案
相关题目
 A.
A. B.
B. C.
C. D.
D. 
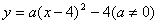 的图象在2<
的图象在2< 的值为【 】
的值为【 】 的图象上,点B,D在反比例函数
的图象上,点B,D在反比例函数 的图象上,AB∥CD∥
的图象上,AB∥CD∥ 的值是
的值是 

 ,在等边三角形ABC中,M、N分别是AB、AC的中点,D是MN上任意一点,CD、BD的延长线分别与AB、AC交于F、E,若
,在等边三角形ABC中,M、N分别是AB、AC的中点,D是MN上任意一点,CD、BD的延长线分别与AB、AC交于F、E,若 ,则等边三角形ABC的边长为
,则等边三角形ABC的边长为
 B.
B.  C.
C.  D.1
D.1
 ,x为自然数),十位上的数字为y,求y与x的函数关系式.
,x为自然数),十位上的数字为y,求y与x的函数关系式.