题目内容
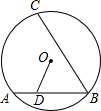 已知:如图,AB,BC为⊙O的弦,点D在AB上,若OD=4,BC=10,∠ODB=∠B=60°,则DB的长为________.
已知:如图,AB,BC为⊙O的弦,点D在AB上,若OD=4,BC=10,∠ODB=∠B=60°,则DB的长为________.
6
分析:延长DO交BC于F,过点O作OE⊥AB点E,OG⊥BC于点G,连接OB,设DB为r;可知△BDF为等边三角形,且OF=r-4,OG=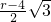 ,结合垂径定理得出BG=5,分别在Rt△OBE中和Rt△OBG中,根据勾股定理列出等式,联立求解即可得出r的值.
,结合垂径定理得出BG=5,分别在Rt△OBE中和Rt△OBG中,根据勾股定理列出等式,联立求解即可得出r的值.
解答: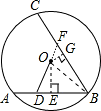 解:延长DO交BC于F,过点O作OE⊥AB点E,OG⊥BC于点G,连接OB,设DB为r;
解:延长DO交BC于F,过点O作OE⊥AB点E,OG⊥BC于点G,连接OB,设DB为r;
又∠ODB=∠B=60°,
故△BDF为等边三角形,
即DB=DF=BF=r;
又OD=4,可得OE=2 ,
,
OF=r-4,OG=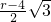 ,
,
又OG⊥BC,且BC=10,
故BG=5;
在Rt△OBE中,OB2=BE2+OE2;
在Rt△OBG中,OB2=BG2+OG2;
代入即可得出
r=6;
即BD=6;
故答案为6.
点评:本题主要考查了垂径定理的应用以及解直角三角形的有关知识,有一定的难度.
分析:延长DO交BC于F,过点O作OE⊥AB点E,OG⊥BC于点G,连接OB,设DB为r;可知△BDF为等边三角形,且OF=r-4,OG=
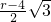 ,结合垂径定理得出BG=5,分别在Rt△OBE中和Rt△OBG中,根据勾股定理列出等式,联立求解即可得出r的值.
,结合垂径定理得出BG=5,分别在Rt△OBE中和Rt△OBG中,根据勾股定理列出等式,联立求解即可得出r的值.解答:
 解:延长DO交BC于F,过点O作OE⊥AB点E,OG⊥BC于点G,连接OB,设DB为r;
解:延长DO交BC于F,过点O作OE⊥AB点E,OG⊥BC于点G,连接OB,设DB为r;又∠ODB=∠B=60°,
故△BDF为等边三角形,
即DB=DF=BF=r;
又OD=4,可得OE=2
 ,
,OF=r-4,OG=
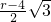 ,
,又OG⊥BC,且BC=10,
故BG=5;
在Rt△OBE中,OB2=BE2+OE2;
在Rt△OBG中,OB2=BG2+OG2;
代入即可得出
r=6;
即BD=6;
故答案为6.
点评:本题主要考查了垂径定理的应用以及解直角三角形的有关知识,有一定的难度.

练习册系列答案
相关题目
 8、已知:如图,AB、AC分别切⊙O于B、C,D是⊙O上一点,∠D=40°,则∠A的度数等于( )
8、已知:如图,AB、AC分别切⊙O于B、C,D是⊙O上一点,∠D=40°,则∠A的度数等于( ) 已知:如图,AB,CD相交于点O,且OA•OD=OB•OC,求证:AC∥DB.
已知:如图,AB,CD相交于点O,且OA•OD=OB•OC,求证:AC∥DB.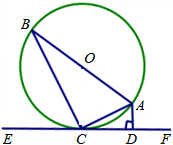 已知:如图,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.
已知:如图,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.
 29、已知,如图,AB∥CD,∠EAB+∠FDC=180°.求证:AE∥FD.
29、已知,如图,AB∥CD,∠EAB+∠FDC=180°.求证:AE∥FD. 已知:如图,AB=AC,DB=DC,求证:∠B=∠C.
已知:如图,AB=AC,DB=DC,求证:∠B=∠C.