题目内容
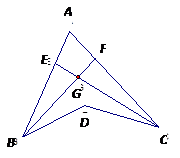
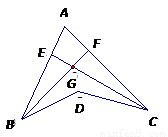
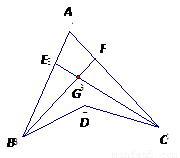
 如图,BF是∠ABD的平分线,CE是∠ACD的平分线,BE与CE交于G,若∠BDC=140°,∠BGC=110°,则∠A的度数为
如图,BF是∠ABD的平分线,CE是∠ACD的平分线,BE与CE交于G,若∠BDC=140°,∠BGC=110°,则∠A的度数为
- A.50°
- B.55°
- C.70°
- D.80°
D
分析:根据三角形内角和定理可求得∠DBC+∠DCB的度数,再根据三角形内角和定理及三角形角平分线的定义可求得∠ABC+∠ACB的度数,从而不难求得∠A的度数.
解答: 解:连接BC.
解:连接BC.
∵∠BDC=140°,
∴∠DBC+∠DCB=180°-140°=40°,
∵∠BGC=110°,
∴∠GBC+∠GCB=180°-110°=70°,
∵BF是∠ABD的平分线,CE是∠ACD的平分线,
∴∠GBD+∠GCD= ∠ABD+
∠ABD+ ∠ACD=30°,
∠ACD=30°,
∴∠ABC+∠ACB=100°,
∴∠A=180°-100°=80°.
故选D.
点评:此题主要考查学生对三角形角平分线的定义及三角形内角和定理的综合运用.
分析:根据三角形内角和定理可求得∠DBC+∠DCB的度数,再根据三角形内角和定理及三角形角平分线的定义可求得∠ABC+∠ACB的度数,从而不难求得∠A的度数.
解答:
 解:连接BC.
解:连接BC.∵∠BDC=140°,
∴∠DBC+∠DCB=180°-140°=40°,
∵∠BGC=110°,
∴∠GBC+∠GCB=180°-110°=70°,
∵BF是∠ABD的平分线,CE是∠ACD的平分线,
∴∠GBD+∠GCD=
 ∠ABD+
∠ABD+ ∠ACD=30°,
∠ACD=30°,∴∠ABC+∠ACB=100°,
∴∠A=180°-100°=80°.
故选D.
点评:此题主要考查学生对三角形角平分线的定义及三角形内角和定理的综合运用.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
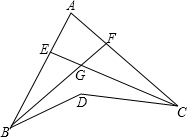 如图,BF是∠ABD的平分线,CE是∠ACD的平分线,BE与CE交于G,若∠BDC=140°,∠BGC=110°,则∠A的度数为( )
如图,BF是∠ABD的平分线,CE是∠ACD的平分线,BE与CE交于G,若∠BDC=140°,∠BGC=110°,则∠A的度数为( )| A、50° | B、55° | C、70° | D、80° |
 如图,BF是∠ABD的平分线,CE是∠ACD的平分线,BF与CE交于G,若∠BDC=130°,∠BGC=100°,则∠A的度数为( )
如图,BF是∠ABD的平分线,CE是∠ACD的平分线,BF与CE交于G,若∠BDC=130°,∠BGC=100°,则∠A的度数为( )