Question

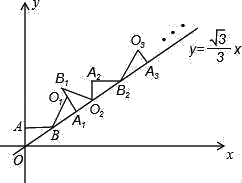
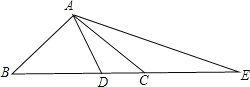
【题目】如图，在等腰与等腰，，，，连接和相交于点，交于点，交与点.下列结论：①；②；③平分；④若，则.其中一定正确的结论的个数是( )

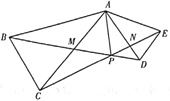
A.1B.2C.3D.4

Answer 1

【答案】C

【解析】

①比较好判断，证明△ABD≌△ACE即可；②错误，用8字模型可求出∠BPE=180°-；③也好判断，全等三角形面积相等，且底边也相等，推出高也相等，利用角平分线的判断定理即可；④构造全等三角形，利用30°角所对的直角边等于斜边的一半转化求解即可.

∵∠BAC=∠DAE=，

∴∠BAC+∠CAD=∠DAE+∠CAD，即∠BAD=∠CAE，

∵AB=AC，AE=AD，

∴△ABD≌△ACE，

∴BD=CE，故①正确.

∵∠EPD+∠ADB+∠PND=180°=∠AEC+∠ANE+∠DAE，∠AEC=∠ADB，∠PND=∠ANE，

∴∠EPD=∠DAE=，

∵∠BPE=180°-∠EPD，

∴∠BPE=180°-，故②错误.

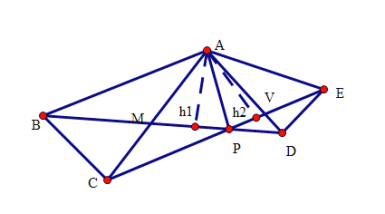
∵全等三角形面积相等，且BD=CE，如图所示，从A点分别作高可知，h1=h2，

∴AP平分∠BPE，故③正确.

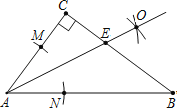
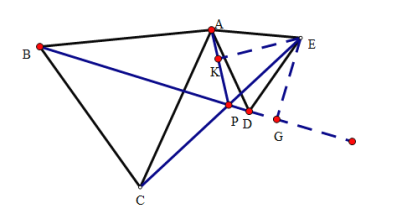
如图所示，从E点引垂线交AP，BD于K、G两点.

∵=60°，

∴由②③可知∠KPE=∠EPG=60°，

∴EK=EG，

∵∠PAD=∠PED，

∴∠PAD+60°=∠PED+60°，即∠EDG=∠EAK，

∴△AKE≌△DGE，

∴AK=DG，

∵∠PEG=90°-60°=30°，

∴KP=PG=PE，

∴PE=AP+PD，故④正确.