ЬтФПФкШн
ЁОЬтФПЁПдФЖСРэНтЬтЃК
бЇЯАСЫЖўДЮИљЪНКѓЃЌФуЛсЗЂЯжвЛаЉКЌгаИљКХЕФЪНзгПЩвдаДГЩСэвЛИіЪНзгЕФЦНЗНЃЌШч![]() ЃЌЮвУЧРДНјаавдЯТЕФЬНЫїЃК
ЃЌЮвУЧРДНјаавдЯТЕФЬНЫїЃК
Щш![]() ЃЈЦфжаaЃЌbЃЌmЃЌnЖМЪЧе§ећЪ§ЃЉЃЌдђга
ЃЈЦфжаaЃЌbЃЌmЃЌnЖМЪЧе§ећЪ§ЃЉЃЌдђга![]() ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ![]() ЃЌетбљОЭЕУГіСЫАбРрЫЦ
ЃЌетбљОЭЕУГіСЫАбРрЫЦ![]() ЕФЪНзгЛЏЮЊЦНЗНЪНЕФЗНЗЈЃЎ
ЕФЪНзгЛЏЮЊЦНЗНЪНЕФЗНЗЈЃЎ
ЧыЗТееЩЯЪіЗНЗЈЬНЫїВЂНтОіЯТСаЮЪЬтЃК
ЃЈ1ЃЉЕБaЃЌbЃЌmЃЌnЖМЪЧе§ећЪ§ЪБЃЌШє![]() ЃЌгУКЌmЃЌnЕФЪНзгЗжБ№БэЪОaЃЌbЃЌЕУa= ЁЁЃЌb=ЁЁ ЁЁЃЛ
ЃЌгУКЌmЃЌnЕФЪНзгЗжБ№БэЪОaЃЌbЃЌЕУa= ЁЁЃЌb=ЁЁ ЁЁЃЛ
ЃЈ2ЃЉРћгУЩЯЪіЗНЗЈЃЌеввЛзще§ећЪ§aЃЌbЃЌmЃЌnЃЌЬюПеЃК
ЁЁ ЁЁЉЁЁ ЁЁ![]() =ЃЈЁЁ ЁЊ
=ЃЈЁЁ ЁЊ ![]() ЃЉ2
ЃЉ2
ЃЈ3ЃЉ![]() ЧвaЃЌmЃЌnЖМЮЊе§ећЪ§ЃЌЧѓaЕФжЕЃЎ
ЧвaЃЌmЃЌnЖМЮЊе§ећЪ§ЃЌЧѓaЕФжЕЃЎ
ЁОД№АИЁП(1)a=m+5n,b=2mn;(2)МћНтЮі;(3)9Лђ21.
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУЭъШЋЦНЗНЙЋЪНАбЃЈm-n![]() ЃЉ2еЙПЊМДПЩЕУЕНгУКЌmЃЌnЕФЪНзгЗжБ№БэЪОГіaЃЌbЃЛ
ЃЉ2еЙПЊМДПЩЕУЕНгУКЌmЃЌnЕФЪНзгЗжБ№БэЪОГіaЃЌbЃЛ
ЃЈ2ЃЉРћгУЃЈ1ЃЉжаЕФБэДяЪНЃЌСюm=2ЃЌn=1ЃЌдђПЩМЦЫуГіЖдгІЕФaКЭbЕФжЕЃЛ
ЃЈ3ЃЉРћгУЃЈ1ЃЉЕФНсЙћЕУЕН2mn=4ЃЌдђmn=2ЃЌдйРћгУmЃЌnЖМЮЊе§ећЪ§ЕУЕНm=2ЃЌn=1Лђm=1ЃЌn=2ЃЌШЛКѓМЦЫуЖдгІЕФaЕФжЕМДПЩЃЎ
(1)Ёп![]() =
=![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉД№АИВЛЮЈвЛ; ШЁm=2ЃЌn=1ЃЌ
дђa=4+5=9ЃЌb=4ЃЛ
(3)Ёп2mn=4ЃЌ
Ёрmn=2ЃЌ
ЖјmЃЌnЖМЮЊе§ећЪ§ЃЌ
Ёрm=2ЃЌn=1Лђm=1ЃЌn=2ЃЌ
ЕБm=2ЃЌn=1ЪБЃЌa=9ЃЛ
ЕБm=1ЃЌn=2ЪБЃЌa=21.
МДaЕФжЕЮЊ9Лђ21.
ЙЪД№АИЮЊЃК(1)a=m+5n,b=2mn;(2)МћНтЮі;(3)9Лђ21.

ЁОЬтФПЁПгаетбљвЛИіЮЪЬтЃКЬНОПКЏЪ§![]() ЕФЭМЯѓгыаджЪЃЎ
ЕФЭМЯѓгыаджЪЃЎ
аЁЛЊИљОнбЇЯАКЏЪ§ЕФОбщЃЌЖдКЏЪ§![]() ЕФЭМЯѓгыаджЪНјааСЫЬНОП.ЯТУцЪЧаЁЛЊЕФЬНОПЙ§ГЬ,ЧыВЙГфЭъећ:
ЕФЭМЯѓгыаджЪНјааСЫЬНОП.ЯТУцЪЧаЁЛЊЕФЬНОПЙ§ГЬ,ЧыВЙГфЭъећ:
(1)КЏЪ§![]() ЕФздБфСПxЕФШЁжЕЗЖЮЇЪЧ ЃЛ
ЕФздБфСПxЕФШЁжЕЗЖЮЇЪЧ ЃЛ
(2)ЯТБэЪЧyгыxЕФМИзщЖдгІжЕ.
x | Ё | -3 | -2 | -1 | 0 |
| 1 | 3 |
| 4 | 5 | 6 | 7 | Ё |
y | Ё |
|
|
|
|
| 6 | 6 |
|
|
|
| m | Ё |
ЧѓmЕФжЕЃЛ
ЃЈ3ЃЉШчЯТЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌУшГіСЫвдЩЯБэжаИїЖдЖдгІжЕЮЊзјБъЕФЕу.ИљОнУшГіЕФЕуЃЌЛГіИУКЏЪ§ЕФЭМЯѓЃЛ
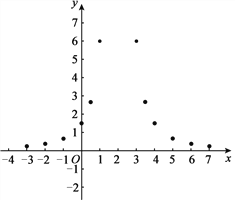
ЃЈ4ЃЉНсКЯКЏЪ§ЕФЭМЯѓЃЌаДГіИУКЏЪ§ЕФвЛЬѕаджЪЃК .