题目内容
已知Rt△ABC的斜边AB=5cm,直角边AC=4cm,BC=3cm,以直线AB为轴旋转一周,得到的几何体的表面积是
- A.22.56πcm2
- B.16.8πcm2
- C.9.6πcm2
- D.7.2πcm2
B
分析:易得此几何体为两个圆锥的组合体,那么表面积为两个圆锥的侧面积,需求得圆锥的底面半径,进而利用圆锥的侧面积=底面周长×母线长÷2即可求得所求的表面积.
解答: 解:以直线AB为轴旋转一周,得到由两个圆锥组成的几何体,
解:以直线AB为轴旋转一周,得到由两个圆锥组成的几何体,
直角三角形的斜边上的高CD= =
= cm,
cm,
则以 为半径的圆的周长=
为半径的圆的周长= πcm,
πcm,
几何体的表面积= π×
π× ×(4+3)=
×(4+3)=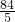 π=16.8πcm2,
π=16.8πcm2,
故选B.
点评:本题利用了圆的周长公式和扇形的面积公式求解.
分析:易得此几何体为两个圆锥的组合体,那么表面积为两个圆锥的侧面积,需求得圆锥的底面半径,进而利用圆锥的侧面积=底面周长×母线长÷2即可求得所求的表面积.
解答:
 解:以直线AB为轴旋转一周,得到由两个圆锥组成的几何体,
解:以直线AB为轴旋转一周,得到由两个圆锥组成的几何体,直角三角形的斜边上的高CD=
 =
= cm,
cm,则以
 为半径的圆的周长=
为半径的圆的周长= πcm,
πcm,几何体的表面积=
 π×
π× ×(4+3)=
×(4+3)=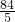 π=16.8πcm2,
π=16.8πcm2,故选B.
点评:本题利用了圆的周长公式和扇形的面积公式求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知Rt△ABC的斜边AB=5,一条直角边AC=3,以直线BC为轴旋转一周得到一个圆锥,则这个圆锥的侧面积为( )
已知Rt△ABC的斜边AB=5,一条直角边AC=3,以直线BC为轴旋转一周得到一个圆锥,则这个圆锥的侧面积为( )| A、8π | B、12π | C、15π | D、20π |
已知Rt△ABC的斜边AB=5cm,直角边AC=4cm,BC=3cm,以直线AB为轴旋转一周,得到的几何体的表面积是( )
| A、22.56πcm2 | B、16.8πcm2 | C、9.6πcm2 | D、7.2πcm2 |
