题目内容

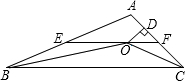
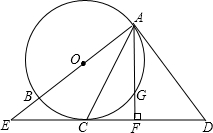
如图，在△ABC中，AB=2，AC=
2
，以A为圆心，1为半径的圆与边BC相切，则BC的长是______．
如图，设线段BC与⊙O相切于点D，连接AD．
∵BC是⊙O的切线，D是切点，
∴AD⊥BC，AD=1．
∴在Rt△ABD中，AB=2，AD=1，∠ADB=90°，BD=
AB2-AD2
=
22-12
=
3
．
在Rt△ACD中，AC=
2
，AD=1，∠ADC=90°，CD=
AC2-AD2
=
(
2
)2-12
=1．
∴BC=BD+CD=1+
3
．
故答案是：1+
3
．
练习册系列答案
相关题目
如图，在△ABC中，∠ABC和∠ACB的平分线相交于点O，过点O作EF∥BC交AB于E，交AC于F，过点O作OD⊥AC于D．下列四个结论：
①EF是△ABC的中位线．
②以E为圆心、BE为半径的圆与以F为圆心、CF为半径的圆外切；
③设OD=m，AE+AF=2n，则S△AEF=mn；
④∠BOC=90°+
1
2
∠A；
其中正确的结论是______．
如图，AB切⊙O于点B，OA=2，∠OAB=30°，弦BC∥OA，劣弧
BC
的弧长为______．（结果保留π）
已知：如图，AB是⊙O的直径，P是AB上的一点（与A、B不重合），QP⊥AB，垂足为P，直线QA交⊙O于C点，过C点作⊙O的切线交直线QP于点D．则△CDQ是等腰三角形．
对上述命题证明如下：
证明：连接OC
∵OA=OC
∴∠A=∠1
∵CD切O于C点
∴∠OCD=90°
∴∠1+∠2=90°
∴∠A+∠2=90°
在Rt△QPA中，∠QPA=90°
∴∠A+∠Q=90°
∴∠2=∠Q
∴DQ=DC
即CDQ是等腰三角形．
问题：对上述命题，当点P在BA的延长线上时，其他条件不变，如图所示，结论“△CDQ是等腰三角形”还成立吗？若成立，请给予证明；若不成立，请说明理由．
（l01l•瑶海区一模）如图，在△七B5中，七B=七5，以七B为直径的⊙O交B5于点D，过点D作EF⊥七5于点E，交七B的延长线于点F．
（1）求证：EF是⊙O的切线；
（l）当七B=5，B5=二时，求DE的长．
矩形ABCD中，AB=8，BC=6，如果圆A是以点A为圆心，9为半径的圆，那么下列判断正确的是（　　）
A．点B、C均在圆A外
B．点B在圆A外、点C在圆A内
C．点B在圆A内、点C在圆A外
D．点B、C均在圆A内
矩形的两邻边长分别为2.5和5，若以较长一边为直径作半圆，则矩形的各边与半圆相切的线段最多有（　　）
A．0条B．1条C．2条D．3条
如图，AB是⊙O的直径，直线AD与⊙O相切于点A，点C在⊙O着，∠DAC=∠ACD，直线DC与AB的延长线交于点E．AF⊥ED于点F，交⊙O于点G．
（k）求证：DE是⊙O的切线；
（2）已知⊙O的半径是6cm，EC=xcm，求GF的长．
如图，PA、PB分别切⊙O于A、B，PA=10cm，C是劣弧AB上的点（不与点A、B重合），过点C的切线分别交PA、PB于点E、F．则△PEF的周长为______cm．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网