题目内容
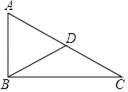
【题目】已知等腰三角形ABC中，AB＝AC，∠ABC＝40°，P为直线BC上一点，PB＝AB，则∠PAC＝_____°．
【答案】30°或120°．
【解析】
分当P点在线段BC上和当P在CB的延长线上两种情况讨论，根据等腰三角形等边对等角，三角形内角和定理和三角形外角定理去求∠PAC的度数.
解：如下图，当P点在线段BC上时，
∵AB=AC，∠ABC=40°，
∴∠C=∠B=40°，
∴∠BAC=100°，
∵BP=AB，
∴∠PAC=∠BAC -
=30°，
如下图，当P在CB的延长线上时，
∵AB=AC，∠ABC=40°，
∴∠C=∠ABC =40°，
∴∠BAC=100°，
∵BP=AB，
∴∠PAC=∠BAC +
=120°．
综上所述：∠PAC的度数为30°或120°，
故答案为：30°或120°.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
