题目内容
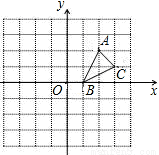
如图，直线y=3x+m交x轴于点A，交y轴于点B（0，3），过A、B两点的抛物线交x轴于另一点C（3，0）．
（1）求抛物线的解析式；
（2）在该抛物线的对称轴上找一点P，使PA+PB最小，求出点P的坐标；
（3）在抛物线的对称轴上是否存在点Q，使△ABQ是等腰三角形？若存在，求出符合条件的Q点坐标；若不存在，请说明理由．
（1）y=-x2+2x+3.（2）P（1，2），（3）Q1（1，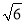
）Q2（1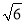，-），Q3（1，0），Q4（1，1）.
【解析】
试题分析：（1）由直线y=3x+m交y轴于点B，求出m的值，可得出A的坐标，把A（-1，0），B（0，3），C（3，0）代入y=ax2+bx+c，即可得出抛物线的解析式，
（2）连接BC，交对称轴一点，此点就是点P，使PA+PB最小，求出直线BC的解析式，再利用对称轴为x=1，即可得出点P的坐标，
（3）利用①当AQ=AB时，△ABQ是等腰三角形，②当BQ=AB时，△ABQ是等腰三角形，③当BQ=AQ时，△ABQ是等腰三角形，分别求出点Q的坐标．
试题解析：（1）∵直线y=3x+m交y轴于点B（0，3），
∴m=3，
∴直线y=3x+3，
∴A（-1，0），
把A（-1，0），B（0，3），C（3，0）代入y=ax2+bx+c，得
，
解得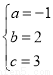
．
∴抛物线的解析式y=-x2+2x+3.
（2）如图1，连接BC，交对称轴一点，此点就是点P，使PA+PB最小，
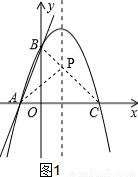
∵A，C关于对称轴对称，
∴此时PA+PB最小，
∵B（0，3），C（3，0）
∴直线BC的解析式为：y=-x+3，
∵对称轴为x=1，
∴P（1，2），
（3）存在
①如图2，当AQ=AB时，△ABQ是等腰三角形，
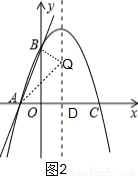
∵AB=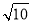
∴AQ=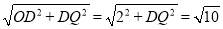
∴DQ=±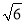
∴Q1（1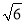，）Q2（1，-）
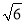②如图3，当BQ=AB时，△ABQ是等腰三角形，
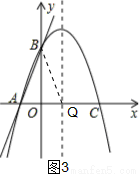
∵OA=1，OQ=1
∴Q3（1，0），
③如图4，当BQ=AQ时，△ABQ是等腰三角形，
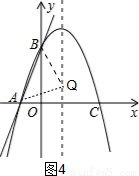
设Q（1，t），
∵A（-1，0），B（0，3），
∴（1+1）2+t2=12+（t-3）2，解得t=1，
∴Q4（1，1）
综上的所述：Q1（1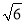，）Q2（1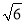，-），Q3（1，0），Q4（1，1）.
考点：二次函数综合题．
