题目内容
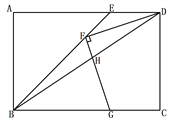
【题目】如图,矩形ABCD中,BE平分∠ABC交AD于点E,F为BE上一点,连接DF,过F作FG⊥DF交BC于点G,连接BD交FG于点H,若FD = FG, ![]() ,BG = 4,则GH的长为__________.
,BG = 4,则GH的长为__________.
【答案】![]()
【解析】过点F作BC的垂线,分别交BC、AD于点M、N,则MN⊥AD,过点A作AP⊥BD于点P,延长DF交AB于点K,过点K作KQ⊥BD于点Q,如图所示。
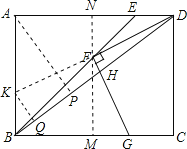
∵FD⊥FG,
∴∠DFG=90°,
∴∠DFN+∠MFG=90°,
∵∠DNF=90°,
∴∠NDF+∠DFN=90°,
∴∠NDF=∠MFG,
在DNF和△FMG中,
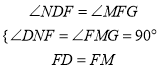 ,
,
∴△DNF≌△FMG(AAS),
∴DN=FM,NF=MG.
∵∠BAD=90°,BE平分∠ABC,
∴∠ABE=∠CBE=45°,
又∵FM⊥BM,
∴FM=BM,
∵BF=![]() ,
,
∴BM=FM=3,MG=BGBM=43=1,
∴NF=MG=1,AB=NM=4,AD=AN+ND=BM+FM=6,
∴BD=![]() .
.
由面积公式可知:S△ABD=![]() BDAP=
BDAP=![]() ABAD,即
ABAD,即![]() AP=4×6,
AP=4×6,
∴AP=![]() ,
,
∵NF∥AB,
∴△DNF∽△DAK,
∴![]() ,
,
∴AK=2NF=2,DK= ![]() =2
=2![]() ,DF=
,DF=![]() =
=![]() .
.
∴BK=ABAK=42=2,
∵KQ∥AP,
∴△BKQ∽△BAP,
∴![]() ,即,
,即, 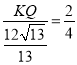 ,
,
∴KQ=![]() ,
,
∴BQ=![]() =
=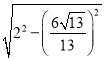 =
=![]() ,
,
∴DQ=BDBQ=![]()
![]() =
=![]() ,
,
∵∠DFH=∠DQK=90°,∠FDH=∠QDK,
∴△DFH∽△DQK,
∴![]() ,
,
即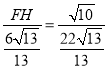 ,
,
∴FH=![]() ,
,
∴GH=FGFH=![]()
![]() =
=![]() .
.
故答案为: ![]()

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目