��Ŀ����
����Ŀ����ѧ���ϣ�����ʦ���������з����е�һ���⣺
С�Ϻ�ͬ��С�����ۺó����½��
��![]() �����������̽������
�����������̽������
����![]() Ϊ
Ϊ![]() ���е�ʱ����ͼ
���е�ʱ����ͼ![]() ��ȷ���߶�
��ȷ���߶�![]() ��
��![]() �Ĵ�С��ϵ������ֱ��д�����ۣ�
�Ĵ�С��ϵ������ֱ��д�����ۣ� ![]() ______
______ ![]() ������
������![]() ����
���� ![]() ����
����![]() ������
������
��![]() �������������������
�������������������
�⣺��Ŀ�У� ![]() ��
��![]() �Ĵ�С��ϵ��
�Ĵ�С��ϵ��![]() __________
__________ ![]() ������
������![]() ����
���� ![]() ����
����![]() �������������£���ͼ
�������������£���ͼ![]() ������
������![]() ��
��![]() ����
����![]() �ڵ�
�ڵ�![]() �������������ɽ������Ľ�����̣���
�������������ɽ������Ľ�����̣���
��![]() ����չ���ۣ��������
����չ���ۣ��������
����������ʦ������������ͽ��ۣ�������ͼ![]() �ڵȱ�������
�ڵȱ�������![]() �У���
����![]() ��
��![]() �ϣ���
�ϣ���![]() ��
��![]() ���ӳ����ϣ���
���ӳ����ϣ���![]() ����ȷ���߶�
����ȷ���߶�![]() ��
��![]() �Ĵ�С��ϵ����˵�����ɣ�
�Ĵ�С��ϵ����˵�����ɣ�
���ڵȱ�������![]() �У���
�У���![]() ��ֱ��
��ֱ��![]() �ϣ���
�ϣ���![]() ��ֱ��
��ֱ��![]() �ϣ���
�ϣ���![]() ����
����![]() �ı߳�Ϊ
�ı߳�Ϊ![]() ��
�� ![]() ����
����![]() �ij�Ϊ__________������ֱ��д���������
�ij�Ϊ__________������ֱ��д���������
��ͼ���ڵȱ�������![]() �У���
����![]() ��
��![]()
�ϣ���![]() ��
��![]() ���ӳ����ϣ���
���ӳ����ϣ���![]() ��
��
��ȷ���߶�![]() ��
��![]() �Ĵ�С��ϵ����˵�����ɣ�
�Ĵ�С��ϵ����˵�����ɣ�
���𰸡���![]() ��
��![]() ����
����![]() ��
��![]() ������������
������������![]() ����
����![]() ����
����![]() ��
��![]() ��
��
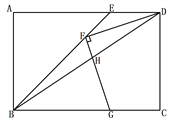
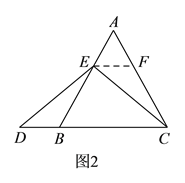
�������������������1�����ݡ�ABC�ǵȱ������Σ���EΪAB���е㣬���ɵó�CE��AB�������ó���ECD=��D�����ɵó��߶�ED��EC�Ĵ�С��ϵ��
��2�����ȵó�BE=CF���������á�DBE�ա�EFC���ɵó�����
��3������![]() ����
����![]() �ڵ�
�ڵ�![]() ����֪
����֪![]() Ϊ�ȱ������Σ�����֤��
Ϊ�ȱ������Σ�����֤��![]() ��
��![]() �����ɵó�
�����ɵó�![]() ��
��
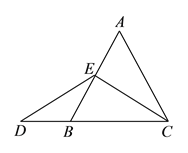
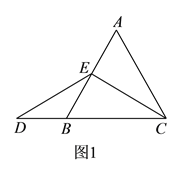
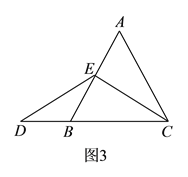
���ֵ�D��CB���ӳ����ϡ���BC���ӳ�������������������ۼ��ɵ�.
�����������![]() ��
��![]() ��
��
��![]() Ϊ�ȱ������Σ�
Ϊ�ȱ������Σ� ![]() ��
��![]() �е㣬��
�е㣬��![]() ��
�� ![]() ��
�� ![]() ��
��
��![]() ����
����![]() ��
��
��![]() ����
����![]() ��
��
��![]() ����
����![]() ��
��
��![]() ��
��![]()
�ڵȱ�![]() �У�
�� ![]() ��
��
��![]() Ϊ�ȱ������Σ�
Ϊ�ȱ������Σ�
��![]() ��
��
����![]() ��
��
��![]() ��
��
����![]() ��
��
��![]() ��
��
ͬ��![]() ��
��
����![]() ��
�� ![]() ��
��
��![]() ��
�� ![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
�У�
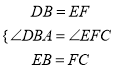 ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ������
������![]() ����
����![]() �ڵ�
�ڵ�![]() ��
��
���֪![]() Ϊ�ȱ������Σ�
Ϊ�ȱ������Σ�
��![]() ��
��
����![]() ��
��
��![]() ��
��
����![]() ��
��
��![]() ��
��
������![]() ��
�� ![]() ��
��
��![]() ��
�� ![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
�У�
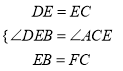 ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��