题目内容
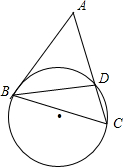如图，AB，AC分别是⊙O的切线和割线，且∠C=45°，∠BDA=60°，CD=
，则切线AB的长是________．
6
分析：过点A作AM⊥BD与点M，在直角△AMD中，AD就可以利用AB表示出来，然后依据切割线定理，即可得到一个关于AB的方程，即可求解．
解答：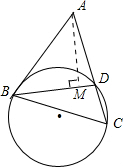
解：
过点A作AM⊥BD与点M．
∵AB为圆O的切线
∴∠ABD=∠C=45°（弦切角等于所夹弧所对的圆周角）
∵∠BDA=60°
∴∠BAD=75°，∠DAM=30°，∠BAM=45°
设AB=x，则AM=
x，在直角△AMD中，AD=
x
由切割线定理得：AB2=AD•AC
x2=x（x+）
解得：x1=6，x2=0（舍去）
故AB=6．
故答案是：6．
点评：本题主要考查了弦切角定理以及切割线定理，根据切割线定理把求线段AB的长的问题转化为方程问题．
分析：过点A作AM⊥BD与点M，在直角△AMD中，AD就可以利用AB表示出来，然后依据切割线定理，即可得到一个关于AB的方程，即可求解．
解答：
解：过点A作AM⊥BD与点M．
∵AB为圆O的切线
∴∠ABD=∠C=45°（弦切角等于所夹弧所对的圆周角）
∵∠BDA=60°
∴∠BAD=75°，∠DAM=30°，∠BAM=45°
设AB=x，则AM=
x，在直角△AMD中，AD=x由切割线定理得：AB2=AD•AC
x2=
x（x+）解得：x1=6，x2=0（舍去）
故AB=6．
故答案是：6．
点评：本题主要考查了弦切角定理以及切割线定理，根据切割线定理把求线段AB的长的问题转化为方程问题．
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
相关题目
8、已知：如图，AB、AC分别切⊙O于B、C，D是⊙O上一点，∠D=40°，则∠A的度数等于（ ）
25、如图，AB、AC分别为⊙O的直径和弦，D为劣弧AC上一点，DE⊥AB于H交⊙O于E，交AC于点F，P为ED延长线上的一点．
如图，AB、AC分别切⊙O于M、N两点，点D在⊙O上，且∠BDC=60°，则∠A=（ ）°．
如图，AB、AC分别为⊙O的内接正六边形、内接正方形的一边，BC是圆内接n边形的一边，则n等于（ ）