题目内容
等腰三角形ABC中AB=AC=13cm，BC=10cm，以A为圆心，11cm为半径的圆与直线BC的位置关系是
- A.相离
- B.相切
- C.相交
- D.无法判断
A
分析：根据等腰三角形的三线合一和勾股定理，求得圆心到直线的距离，再根据数量关系进行判断．若d＜r，则直线与圆相交；若d=r，则直线于圆相切；若d＞r，则直线与圆相离．
解答：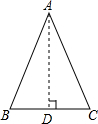
解：作AD⊥BC于D．
根据等腰三角形的三线合一，得BD=5cm；
再根据勾股定理得AD=12cm，
∵12cm＞11cm
∴以11cm为半径的⊙A与BC所在直线的位置关系是相离．
故选：A．
点评：此题考查了直线和圆的位置关系与数量之间的联系．能够综合运用等腰三角形的性质和勾股定理求解．
分析：根据等腰三角形的三线合一和勾股定理，求得圆心到直线的距离，再根据数量关系进行判断．若d＜r，则直线与圆相交；若d=r，则直线于圆相切；若d＞r，则直线与圆相离．
解答：
解：作AD⊥BC于D．根据等腰三角形的三线合一，得BD=5cm；
再根据勾股定理得AD=12cm，
∵12cm＞11cm
∴以11cm为半径的⊙A与BC所在直线的位置关系是相离．
故选：A．
点评：此题考查了直线和圆的位置关系与数量之间的联系．能够综合运用等腰三角形的性质和勾股定理求解．
练习册系列答案
一线名师权威作业本系列答案
相关题目
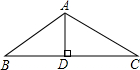如图所示，在等腰三角形ABC中，AB=AC=12cm，∠ABC=30°，那么底边上的高AD=
如图，等腰三角形ABC中，AB=AC，AD是底边BC上的中线，若AB=10，BC=12，则中线AD的长度为（ ）