题目内容
三角形的三边为a，b，c，由下列条件不能判断它是直角三角形的是
- A.a：b：c=8：16：17
- B.a2-b2=c2
- C.a2=（b+c）（b-c）
- D.a：b：c=13：5：12
A
分析：根据勾股定理的逆定理进行分析，从而得到答案．
解答：A、因为82+162≠172，所以不是直角三角形；
B、因为a2-b2=c2即c2+b2=a2，所以是直角三角形；
C、因为a2=（b+c）（b-c），即a2+c2=b2，所以是直角三角形；
D、因为52+122=132，所以是直角三角形．
故选A．
点评：解答此题要用到勾股定理的逆定理：已知三角形ABC的三边满足a2+b2=c2，则三角形ABC是直角三角形．
分析：根据勾股定理的逆定理进行分析，从而得到答案．
解答：A、因为82+162≠172，所以不是直角三角形；
B、因为a2-b2=c2即c2+b2=a2，所以是直角三角形；
C、因为a2=（b+c）（b-c），即a2+c2=b2，所以是直角三角形；
D、因为52+122=132，所以是直角三角形．
故选A．
点评：解答此题要用到勾股定理的逆定理：已知三角形ABC的三边满足a2+b2=c2，则三角形ABC是直角三角形．
练习册系列答案
相关题目
（一）小明在玩积木游戏时，把三个正方形积木摆成一定的形状，正视图如图①，
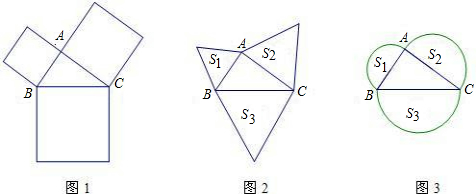
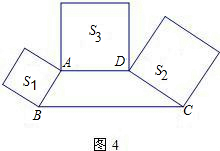梯形外作正方形，其面积分别为S1、S2、S3，则S1、S2、S3之间的数量关系式为
（2012•新疆）如图所示，分别以直角三角形的三边为直径作半圆，其中两个半圆的面积