题目内容
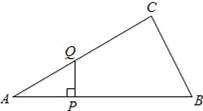
若AD∥BE,且∠ACB=90°,∠CBE=30°,则∠CAD的度数为( )
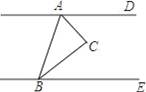

A.30° B.40° C.50° D.60°
D【考点】平行线的性质.
【分析】延长AC交BE于F,根据直角三角形两锐角互余求出∠1,再根据两直线平行,内错角相等可得∠CAD=∠1.
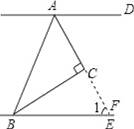
【解答】解:如图,延长AC交BE于F,
∵∠ACB=90°,∠CBE=30°,
∴∠1=90°﹣30°=60°,
∵AD∥BE,
∴∠CAD=∠1=60°.
故选D.

【点评】本题考查了平行线的性质,直角三角形两锐角互余的性质,熟记性质是解题的关键.

练习册系列答案
相关题目
某校初三(1)班50名学生需要参加体育“五选一”自选项目测试,班上学生所报自选项目的情况统计表如下:
| 自选项目 | 人数 | 频率 |
| 立定跳远 | 9 | 0.18 |
| 三级蛙跳 | 12 | a |
| 一分钟跳绳 | 8 | 0.16 |
| 投掷实心球 | b | 0.32 |
| 推铅球 | 5 | 0.10 |
| 合计 | 50 | 1 |
(1)求a,b的值;
(2)若将各自选项目的人数所占比例绘制成扇形统计图,求“一分钟跳绳”对应扇形的圆心角的度数;
(3)在选报“推铅球”的学生中,有3名男生,2名女生,为了了解学生的训练效果,从这5名学生中随机抽取两名学生进行推铅球测试,求所抽取的两名学生中

 有一名女生的概率.
有一名女生的概率.

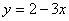 ;②
;②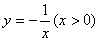 ;③
;③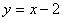 ;④
;④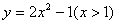 ,
,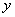 随
随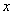 的增大而增大的函数有
的增大而增大的函数有  ,按标价的6折销售可赚80元,__________________
,按标价的6折销售可赚80元,__________________ ),B(
),B(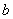 ,0),C
,0),C (0,
(0,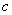 ),
),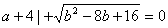 ,
,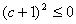 ,点D与
,点D与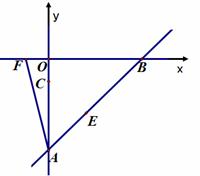

 B.
B.
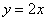 与双曲线
与双曲线 的一个交点是
的一个交点是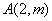 ,则点
,则点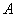 的坐标是 ,双曲线
的坐标是 ,双曲线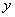 = .
= .