��Ŀ����
ijУ������1����50��ѧ����Ҫ�μ���������ѡһ����ѡ��Ŀ���ԣ�����ѧ��������ѡ��Ŀ�����ͳ�Ʊ����£�
| ��ѡ��Ŀ | ���� | Ƶ�� |
| ������Զ | 9 | 0.18 |
| �������� | 12 | a |
| һ�������� | 8 | 0.16 |
| Ͷ��ʵ���� | b | 0.32 |
| ��Ǧ�� | 5 | 0.10 |
| �ϼ� | 50 | 1 |
��1����a��b��ֵ��
��2����������ѡ��Ŀ��������ռ�������Ƴ�����ͳ��ͼ����һ������������Ӧ���ε�Բ�ĽǵĶ�����
��3����ѡ������Ǧ��ѧ���У���3��������2��Ů����Ϊ���˽�ѧ����ѵ��Ч��������5��ѧ���������ȡ����ѧ��������Ǧ����ԣ�������ȡ������ѧ����

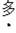
 ��һ��Ů���ĸ��ʣ�
��һ��Ů���ĸ��ʣ�
�����㡿��Ϸ��ƽ�ԣ���ö�ٷ�������ͳ��ͼ��
��ר�⡿ͼ���ͣ�
����������1�����ݱ������a��b��ֵ���ɣ�
��2�����ݱ�ʾ��������ͳ��ͼ�������һ������������Ӧ���ε�Բ�ĽǵĶ������ɣ�
��3���б��ó����еȿ��ܵ���������ҳ���ȡ������ѧ����������һ��Ů����������������������ʣ�
����𡿽⣺��1����������ã�a=1����0.18+0.16+0.32+0.10��=0.24��
b=
 ��0.32=16��
��0.32=16��
��2����������ͳ��ͼ����ͼ��ʾ��


��������ã�360���0.16=57.6�㣻
��3���������ΪA��B��C��Ů�����ΪD��E��
��ö�ٷ��ɵã�AB��AC��AD��AE��BC��BD��BE��CD��CE��DE��10�֣�����DEΪŮŮ��ϣ�AB��AC��BC��������ϣ�
���ȡ������ѧ����������һ��Ů���ĸ���Ϊ��
 ��
��
�����������⿼������Ϸ��ƽ�ԣ�����ͳ��ͼ���б�������״ͼ����Ū�������ǽⱾ��Ĺؼ���




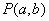 �Ƿ���������
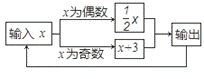
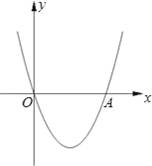
�Ƿ���������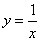 ͼ�������ڵ�(һ1����1)��һ�����㣬��
ͼ�������ڵ�(һ1����1)��һ�����㣬��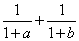 ��ֵΪ ( )
��ֵΪ ( )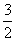 D.
D. 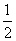
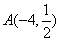 ��
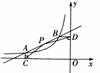
�� ��һ�κ���
��һ�κ���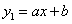 �뷴��������
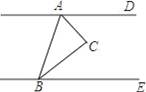
�뷴��������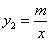 ͼ����������㣬
ͼ����������㣬 ���ڵ�
���ڵ�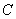 ,
,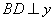 ���ڵ�
���ڵ�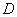 .
.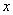 ȡ��ֵʱ��
ȡ��ֵʱ��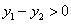 ?
?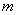 ��ֵ. ��23��
��ֵ. ��23��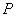 ���߶�
���߶�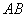 ��һ�㣬����
��һ�㣬����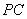 ��
��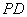 ����
����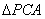 ��
��
 Լ�ֵ� .
Լ�ֵ� .