题目内容
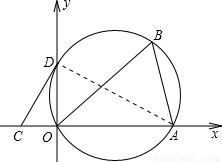
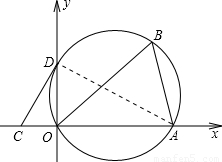
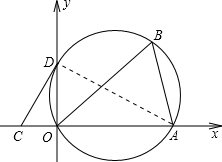
如图，将△AOB置于直角坐标系中，O为原点，A（3，0），∠ABO=60°．若△AOB的外接圆与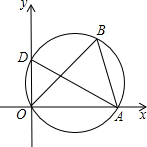
y轴交于点D．（1）直接写出∠ADO的度数．
（2）求△AOB的外接圆半径r．
分析：（1）根据同弧所对的圆周角相等即可得出结论．
（2）如果设三角形AOB外接圆的圆心为M，有了∠ADO的度数，就能求出∠OMA的度数，如果过M作OA的垂线，在形成的直角三角形中，就能根据三角形函数和A的坐标求出半径的长．
（2）如果设三角形AOB外接圆的圆心为M，有了∠ADO的度数，就能求出∠OMA的度数，如果过M作OA的垂线，在形成的直角三角形中，就能根据三角形函数和A的坐标求出半径的长．
解答：
解：（1）∠ADO=60°；
（2）设三角形AOB外接圆的圆心为M，连接OM，过M作MN⊥OA于N，那么
∠OMN=∠OBA=60°，ON=
OA=
；
直角三角形OMN中，
OM=ON÷sin60°=
÷
=
，
因此三角形AOB外接圆的半径r=
．
解：（1）∠ADO=60°；（2）设三角形AOB外接圆的圆心为M，连接OM，过M作MN⊥OA于N，那么
∠OMN=∠OBA=60°，ON=
| 1 |
| 2 |
| 3 |
| 2 |
直角三角形OMN中，
OM=ON÷sin60°=
| 3 |
| 2 |
| ||
| 2 |
| 3 |
因此三角形AOB外接圆的半径r=
| 3 |
点评：本题主要考查了圆周角定理，三角形的外接圆及外心等知识点；据圆周角定理得出相等角的度数，是解题的关键．
练习册系列答案
53随堂测系列答案
相关题目
，0），∠ABO=60度．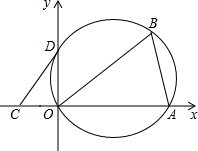
如图，将△AOB置于平面直角坐标系中，其中点O为坐标原点，点A的坐标为（3，0），∠ABO=60°．
