题目内容
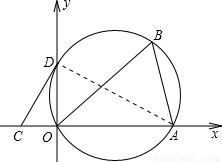
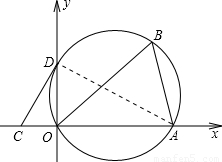
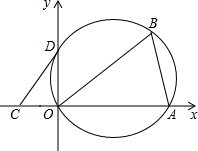 如图,将△AOB置于平面直角坐标系中,其中点O为坐标原点,点A的坐标为(3,0),∠ABO=60°.
如图,将△AOB置于平面直角坐标系中,其中点O为坐标原点,点A的坐标为(3,0),∠ABO=60°.(1)求作△AOB的外接圆圆心P,并求出P点的坐标;
(2)若⊙P与y轴交于点D,求D点的坐标;
(3)若CD是⊙P的切线,求直线CD的函数解析式.
分析:(1)设⊙P与y轴交于D点,连接AD,因为∠AOD=90°,根据圆周角定理可知,AD为⊙O的直径,则圆心P为AD的中点,利用解直角三角形 求OD,再利用中点坐标公式求P点坐标.
(2)在直角三角形ADO中,因为∠ADO=∠ABO=60°,OA=3,然后即可求出OD,即得D点的坐标.
(3)连接PO,先求出C点的坐标,再利用待定系数法求出直线CD的解析式.
(2)在直角三角形ADO中,因为∠ADO=∠ABO=60°,OA=3,然后即可求出OD,即得D点的坐标.
(3)连接PO,先求出C点的坐标,再利用待定系数法求出直线CD的解析式.
解答:解:(1)连接AD,则圆心P为AD的中点,
在直角三角形ADO中,∠ADO=∠ABO=60°,
∴tan60°=
,则OD=
=
,
∴P点的坐标为(
,
).
(2)在直角三角形ADO中,
∵∠ADO=∠ABO=60°,OA=3,
∴tan60°=
,
∴OD=
,
∴D点的坐标为(0,
);
(3)连接PO,则PD=PO;
∵∠PAO=90°-60°=30°,
∠POD=∠PDO=60°,
∵CD是⊙P的切线,
∴∠PDC=90°,
∴∠CDO=30°,
∴在Rt△DCO中,tan30°=
,OD=
,
∴OC=1,
∴C点的坐标为(-1,0);
可设直线CD的解析式为y=kx+b,
将C,D两点的坐标代入解析式,解得
,
∴直线CD的解析式:y=
x+
.
在直角三角形ADO中,∠ADO=∠ABO=60°,
∴tan60°=
| AO |
| OD |
| 3 | ||
|
| 3 |
∴P点的坐标为(
| 3 |
| 2 |
| ||
| 2 |
(2)在直角三角形ADO中,
∵∠ADO=∠ABO=60°,OA=3,
∴tan60°=
| OA |
| OD |
∴OD=
| 3 |
∴D点的坐标为(0,
| 3 |
(3)连接PO,则PD=PO;
∵∠PAO=90°-60°=30°,

∠POD=∠PDO=60°,
∵CD是⊙P的切线,
∴∠PDC=90°,
∴∠CDO=30°,
∴在Rt△DCO中,tan30°=
| OC |
| OD |
| 3 |
∴OC=1,
∴C点的坐标为(-1,0);
可设直线CD的解析式为y=kx+b,
将C,D两点的坐标代入解析式,解得
|
∴直线CD的解析式:y=
| 3 |
| 3 |
点评:本题主要是考查圆的切线性质,圆周角定理,三角形的外接圆及待定系数法.解题的关键是利用数形结合的思想,将形的问题转化为代数方法来解题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
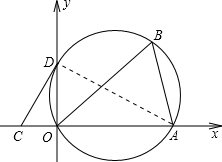 ,0),∠ABO=60度.
,0),∠ABO=60度.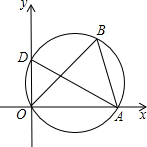 y轴交于点D.
y轴交于点D.