��Ŀ����
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�������y=ax2+bx+c��ԭ��O��B����4��4�����ҶԳ���Ϊֱ��x=![]() ��
��
��1���������ߵĺ�������ʽ��
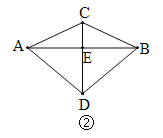
��2��D��ֱ��OB�·��������ϵ�һ���㣬����OD��BD���ڵ�D�˶������У�����OBD������ʱ�����D���������OBD����������
��3����ͼ2������PΪƽ����һ�㣬��N���������ϣ��ҡ�NBO=��ABO�����ڣ�2���������£�ֱ��д��������POD�ס�NOB�ĵ�P���꣮

���𰸡���1��y=x2+3x����2����m=��2ʱ��S��BOD�����ֵ�����ֵΪ8����ʱD������Ϊ����2����2������3��P������Ϊ��![]() ����
����![]() ����
����![]() ��
��![]() ����
����
��������
�����������ô���ϵ�����Ϳ���������ߵĽ���ʽ��
��D����DC��y�ύOB��C�������D��m��m2+3m������4��m��0������C��m����m���������������������ʽ���㻯��S��BOD=��2��m+2��2+8����������.
��BK��y����K��BI��x����I��BN��y����M�㣬���ı���BIOKΪ�����Σ�������ȫ�������ж������ó�Rt��BIA��Rt��BKM���г�������![]() �����ã�2���������������ۼ������.
�����ã�2���������������ۼ������.
�⣺��1���������߶Գ���Ϊֱ��x=![]() ��
��
��A����3��0����
�������߽���ʽΪy=ax��x+3����
��B����4��4�������a����4������4+3��=4�����a=1��
�������߽���ʽΪy=x��x+3������y=x2+3x��
��2����D����DC��y�ύOB��C����ͼ1��
ֱ��OB�Ľ���ʽΪy=��x��
��D��m��m2+3m������4��m��0������C��m����m����
��DC=��m����m2+3m��=��m2��4m��
��S��BOD=S��BCD+S��OCD=![]() 4DC=��2m2��8m=��2��m+2��2+8��
4DC=��2m2��8m=��2��m+2��2+8��
��m=��2ʱ��S��BOD�����ֵ�����ֵΪ8����ʱD������Ϊ����2����2����
��3����BK��y����K��BI��x����I��BN��y����M�㣬��ͼ2��
���ı���BIOKΪ��������
�ߡ�NBO=��ABO��
���IBA=��KBM��
��BI=KM��
��Rt��BIA��Rt��BKM��
��KM=AI=1��
��M��0��3����
��ֱ��BN�Ľ���ʽΪy=px+q��
��B����4��4����M��0��3�������![]() �����
�����![]() ��
��
��ֱ��BN�Ľ���ʽΪy=��![]() x+3��
x+3��
�ⷽ���� ��
��![]() ��
��![]() ��
��
��N��![]() ��
��![]() ����
����
��OB=4![]() ��OD=2
��OD=2![]() ��
��
��![]() =
=![]() ��
��
���POD����NOB�����Ʊ�Ϊ1��2��
��OB���е�E��EF��BN��ON��F����ͼ2��
���FOE�ס�NOB�����ǵ����Ʊ�Ϊ1��2��
��F��ΪON���е㣬
��F��![]() ��
��![]() ����
����
�ߵ�E���D����x��Գƣ�
���P�����F����x��Գ�ʱ����P��OD�ա�FOE������P��OD�ס�NOB����ʱP�䣨![]() ����
����![]() ����
����
��P�������OD�ĶԳƵ�P��������P��OD�ա�P��OD������P��OD�ס�NOB����ʱP�壨��![]() ��
��![]() ����
����
��������������������P��������![]() ����
����![]() ����
����![]() ��
��![]() ����
����