题目内容
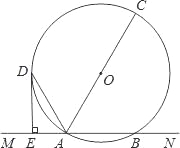
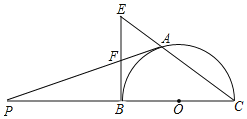
【题目】如图,BC是半⊙O的直径,A是⊙O上一点,过点的切线交CB的延长线于点P,过点B的切线交CA的延长线于点E,AP与BE相交于点F.
(1)求证:BF=EF;
(2)若AF=![]() ,半⊙O的半径为2,求PA的长度.
,半⊙O的半径为2,求PA的长度.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)连接OA,可得∠E+∠C=∠EAF+∠OAC=90°,再根据OA=OC,即可解答
(2)连接AB,可得∠OAP=∠OBE=90°,且BF=AF=1.5,根据三角函数求出PB=![]() ,
,
再证明△APB∽△CPA,即可解答
(1)证明:连接OA,
∵AF、BF为半⊙O的切线,
∴AF=BF,∠FAO=∠EBC=90°,
∴∠E+∠C=∠EAF+∠OAC=90°,
∵OA=OC,
∴∠C=∠OAC,
∴∠E=∠EAF,
∴AF=EF,
∴BF=EF;
(2)解:连接AB,
∵AF、BF为半⊙O的切线,
∴∠OAP=∠OBE=90°,且BF=AF=1.5,
又∵tan∠P=![]() ,即
,即![]() ,
,
∴PB=![]() ,
,
∵∠PAE+∠OAC=∠AEB+∠OCA=90°,且∠OAC=∠OCA,
∴∠PAE=∠AEB,∠P=∠P,
∴△APB∽△CPA,
∴![]() ,即PA2=PBPC,
,即PA2=PBPC,
∴![]() ,解得PA=
,解得PA=![]() .
.![]()

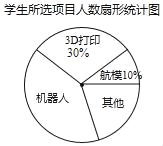
【题目】初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.
男、女生所选项目人数统计表
项目 | 男生(人数) | 女生(人数) |
机器人 | 7 | 9 |
3D打印 | m | 4 |
航模 | 2 | 2 |
其他 | 5 | n |
根据以上信息解决下列问题:
(1)m=_____,n=_____;
(2)扇形统计图中机器人项目所对应扇形的圆心角度数为_____°;
(3)从选航模项目的4名学生中随机选取2名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的2名学生中恰好有1名男生、1名女生的概率.