题目内容
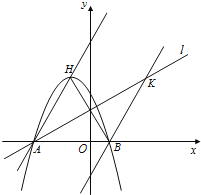
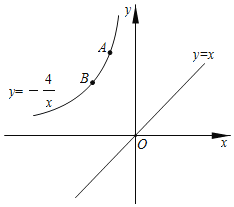
【题目】如图，反比例函数y＝﹣
在第二象限的图象上有两点A、B，它们的横坐标分别为﹣1、﹣2，在直线y＝x上求一点P，使PA+PB最小．则P点坐标为（ ）
A. P（
，）B. P（
，）C. P（1，1）D. P（
，）
【答案】B
【解析】
由题意可求点A、B的坐标，再根据对称，找出其中一点关于直线y＝x对称的点坐标，直线AC与直线y＝x交点就是所求的点P，组成方程组求解即可．
解：把A、B的横坐标分别为﹣1、﹣2分别代入反比例函数y＝﹣
得：
把A、B的纵坐标分别为4、2，
∴A（﹣1，4）B（﹣2，2），
由题意得：点B关于y＝x对称的点C，直线AC与直线y＝x的交点即为的P；
B（﹣2，2）关于y＝x对称的点C（2，﹣2），
设直线AC的关系式为y＝kx+b，由题意得：
解得：
，
∴直线AC的关系式为y＝﹣2x+2，
∵
的解为：
，
∴点P（
，）
故选：B．
练习册系列答案
相关题目
