Question

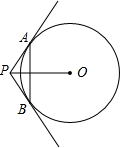
5、如图，直线PA、PB、MN分别与⊙O相切于点A、B、D，若PA=PB=8cm，则△PMN的周长是

16cm

．如图，PA，PB分别切⊙O于A、B两点，C是⊙O上一点，∠P=50°，则∠ACB的度数是

65°

．

Answer 1

分析：（1）依据圆的切线的性质，可推出MA=MD，ND=NB，所以△PMN的周长=PM+MD+DN+PN=PA+PB，再由PA、PB的长度，即可推出△PMN的周长，（2）连接OA、OB，根据切线的性质定理，结合四边形AOBP的内角和为360°，即可推出∠AOB的度数，然后根据圆周角定理，即可推出∠C的度数．

解答：解：（1）∵直线PA、PB、MN分别与⊙O相切，
∴MA=MD，ND=NB，
∵△PMN的周长=PM+PN+MN，
∴△PMN的周长=PM+MP+BN+PN=PA+PB，
∵PA=PB=8cm，
∴△PMN的周长=16cm．

（2）连接OA、OB，
∵直线PA、PB分别与⊙O相切于点A、B，
∴OA⊥PA，OB⊥PB，
∵∠P=50°，
∴∠AOB=130°，
∵C是⊙O上一点，
∴∠ACB=65°．

故答案为16cm，65°．

点评：本题主要考查切线的性质、四边形的内角和、圆周角定理，关键在于熟练灵活运用切线的性质，通过作辅助线构建四边形，最后通过圆周角定理即可推出结果．