题目内容
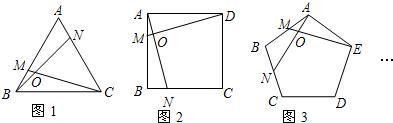
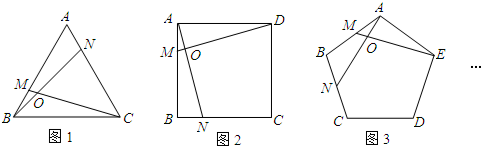
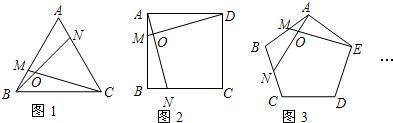
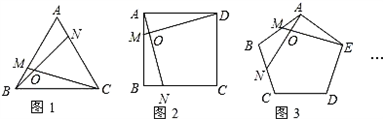
 如图,正九边形ABCDEFGHI中,AE=1,那么AB+AC的长是________.
如图,正九边形ABCDEFGHI中,AE=1,那么AB+AC的长是________.
1
分析:先由多边形的内角和定理,求出正九边形内角的度数,由圆周角定理可求出∠CAB=20°,连接AH,作HM,GN分别垂直AE于M,N,再求出△AHM中各角的度数,由正方形的性质及直角三角形的性质即可解答.
解答:∵正九边形内角和为(9-2)×180°=1260°,
∴每个内角为140°,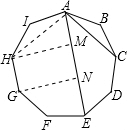
又∵AB=AC,∠B=140°,
∴∠CAB=(180°-140°)÷2=20°,
连接AH,作HM,GN分别垂直AE于M,N.
∵∠CAE=2∠CAB=2×20°=40°.
∴∠HAM=140°-2×20°-40°=60°,
∴∠AHM=30°,
设AM=EN=x,MN=y,
四边形HGNM是矩形,所以HG=y,即正九边形边长为y,
在Rt△AHM中,∠AHM=∠30°,
∴AH=2AM=2x,
∴AB+AC=y+2x,
而x+y+x=1,
∴2x+y=1,
∴AB+AC=1.
故答案为:1.
点评:本题考查的是正多边形和圆及直角三角形的性质,根据题意作出辅助线是解答此题的关键.
分析:先由多边形的内角和定理,求出正九边形内角的度数,由圆周角定理可求出∠CAB=20°,连接AH,作HM,GN分别垂直AE于M,N,再求出△AHM中各角的度数,由正方形的性质及直角三角形的性质即可解答.
解答:∵正九边形内角和为(9-2)×180°=1260°,
∴每个内角为140°,

又∵AB=AC,∠B=140°,
∴∠CAB=(180°-140°)÷2=20°,
连接AH,作HM,GN分别垂直AE于M,N.
∵∠CAE=2∠CAB=2×20°=40°.
∴∠HAM=140°-2×20°-40°=60°,
∴∠AHM=30°,
设AM=EN=x,MN=y,
四边形HGNM是矩形,所以HG=y,即正九边形边长为y,
在Rt△AHM中,∠AHM=∠30°,
∴AH=2AM=2x,
∴AB+AC=y+2x,
而x+y+x=1,
∴2x+y=1,
∴AB+AC=1.
故答案为:1.
点评:本题考查的是正多边形和圆及直角三角形的性质,根据题意作出辅助线是解答此题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目