题目内容
阅读并完成填空.
九年级数学兴趣小组展示了他们小组探究的过程和发现的结果,内容如下:
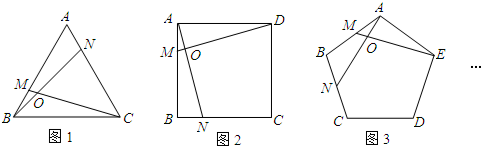
(1)如图1,正三角形ABC中,在AB、AC边上分别取点M、N,使BM=AN,连接BN、CM,发现BN=CM,当M、N改变位置且保持BM=AN时,∠NOC保持不变,请猜测∠NOC的度数:∠NOC=
(2)如图2,正方形ABCD中,在AB、BC边上分别取点M、N,使AM=BN,连接AN、DM,那么AN=DM,且∠DON=
(3)如图3,正五边形ABCDE中,在AB、BC边上分别取点M、N,使AM=BN,连接AN、EM,那么AN=EM,且∠EON=
(4)在正n边形中,对相邻的三边实施同样的操作过程,也会有类似的结论.请大胆猜测,用一句话概括你的发现:
九年级数学兴趣小组展示了他们小组探究的过程和发现的结果,内容如下:

(1)如图1,正三角形ABC中,在AB、AC边上分别取点M、N,使BM=AN,连接BN、CM,发现BN=CM,当M、N改变位置且保持BM=AN时,∠NOC保持不变,请猜测∠NOC的度数:∠NOC=
60
60
度.(2)如图2,正方形ABCD中,在AB、BC边上分别取点M、N,使AM=BN,连接AN、DM,那么AN=DM,且∠DON=
90
90
度.(3)如图3,正五边形ABCDE中,在AB、BC边上分别取点M、N,使AM=BN,连接AN、EM,那么AN=EM,且∠EON=
108
108
度.(4)在正n边形中,对相邻的三边实施同样的操作过程,也会有类似的结论.请大胆猜测,用一句话概括你的发现:
以上所求的角恰好等于正n边形的内角
| (n-2)•180° |
| n |
以上所求的角恰好等于正n边形的内角
.| (n-2)•180° |
| n |
分析:(1)根据等边三角形的性质得出∠A=∠CBM,AB=BC,进而利用全等三角形的判定与性质得出,∠OBC+∠BCM=∠NOC=60°;
(2)根据正方形的性质以及全等三角形的判定与性质得出,∠DON=∠AMD+∠BAN=90°;
(3)根据正五边形的性质以及全等三角形的判定与性质得出,∠EON=∠AEM+∠EOA=108°;
(4)根据以上所求得出在正n边形中,类似的结论.
(2)根据正方形的性质以及全等三角形的判定与性质得出,∠DON=∠AMD+∠BAN=90°;
(3)根据正五边形的性质以及全等三角形的判定与性质得出,∠EON=∠AEM+∠EOA=108°;
(4)根据以上所求得出在正n边形中,类似的结论.
解答:解:(1)∵正三角形ABC中,在AB、AC边上分别取点M、N,使BM=AN,
∴∠A=∠CBM,AB=BC,
∵在△ABN和△BCM中
,
∴△ABN≌△BCM(SAS),
∴∠ABN=∠MCB,
∴∠OBC+∠BCM=∠NOC=60°,
故答案为:60;
(2)∵在正方形ABCD中,在AB、BC边上分别取点M、N,使AM=BN,
∴AD=AB,
∵在△ABN和△DAM中,
,
∴△ABN≌△DAM(SAS),
∴∠AMD=∠ANB,∠ADM=∠BAN,
∴∠DON=∠AMD+∠BAN=90°,
故答案为:90;
(3)∵在正五边形中,在AB、BC边上分别取点M、N,使AM=BN,
∴AB=AE,∠EAM=∠ANB,
∵在△AEM和△BAN中
,
∴△ABN≌△EAM(SAS),
∴∠AEM=∠BAN,
∴∠EON=∠AEM+∠EOA=108°,
故答案为:108;
(4)∵正三角形的内角度数为:60°,正方形的内角度数为:90°,正五边形的内角度数为:108°,
∴以上所求的角恰好等于正n边形的内角
.
故答案为:以上所求的角恰好等于正n边形的内角
.
∴∠A=∠CBM,AB=BC,
∵在△ABN和△BCM中
|
∴△ABN≌△BCM(SAS),
∴∠ABN=∠MCB,
∴∠OBC+∠BCM=∠NOC=60°,
故答案为:60;
(2)∵在正方形ABCD中,在AB、BC边上分别取点M、N,使AM=BN,
∴AD=AB,
∵在△ABN和△DAM中,
|
∴△ABN≌△DAM(SAS),
∴∠AMD=∠ANB,∠ADM=∠BAN,
∴∠DON=∠AMD+∠BAN=90°,
故答案为:90;
(3)∵在正五边形中,在AB、BC边上分别取点M、N,使AM=BN,
∴AB=AE,∠EAM=∠ANB,
∵在△AEM和△BAN中
|
∴△ABN≌△EAM(SAS),
∴∠AEM=∠BAN,
∴∠EON=∠AEM+∠EOA=108°,
故答案为:108;
(4)∵正三角形的内角度数为:60°,正方形的内角度数为:90°,正五边形的内角度数为:108°,
∴以上所求的角恰好等于正n边形的内角
| (n-2)•180° |
| n |
故答案为:以上所求的角恰好等于正n边形的内角
| (n-2)•180° |
| n |
点评:此题主要考查了正多边形的性质以及全等三角形的判定与性质等知识,利用三角形的外角性质得出是解题关键.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
 17、说理题:
17、说理题: